Page 183 - 《应用声学》2023年第6期

第 42 卷 第 6 期 赵晓静等： 基于频谱 Sevcik 维数的目标运动速度估计 1293

1.0 SNR下，多普勒的存在对频谱 Sevcik维数的影响明

显大于频谱熵(如图7(c)所示)。
0.8
100
0.6
ॆʷӑϙ 0.4 80 ྅
Sevcik፥஝

0.2 60
྅ ᤴएឨࣀ/%
Sevcik፥஝ 40
0
0 5 10 15 20
ᤴए/(mSs -1 ) 20

图 5 熵和 Sevcik 搜索结果对比 0
-30 -20 -10 0 10 20
Fig. 5 Comparision of estimation result of entropy
η٪උ/dB
and Sevcik
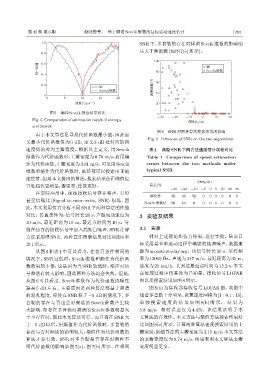
图 6 SNR 对两种算法搜索结果的影响
由于本文算法是寻找代价函数最小值，因此定
Fig. 6 Influence of SNR on the two algorithms
义最小代价函数值为 0 dB，定义 3 dB 处对应的两
速度值的差为主瓣宽度。根据以上定义，用 Sevcik 表 1 典型 SNR 下两方法速度估计误差对比
维数作为代价函数时，主瓣宽度为0.76 m/s，而用熵 Table 1 Comparison of speed estimation
作为代价函数，主瓣宽度为3.81 m/s。可见用Sevcik errors between the two methods under
维数和熵作为代价函数时，虽然都可以搜索出正确 typical SNR
速度值，但是本文提出的算法，搜索结果在正确值位
SNR/dB
置处起伏更明显，瓣更窄，性能更好。 误差/%
−30 −20 −10 −5 0 5 10 20 30
在实际应用中，往往接收信号存在噪声，有时
熵值法 50 30 56 0 0 0 0 0 0
甚至信噪比 (Signal to noise ratio, SNR) 很低，因
Sevcik 维数法 56 54 0 0 0 0 0 0 0
此，本文利用仿真分析不同SNR下两种算法的性能
对比。仿真条件为：信号时长 20 s，声源运动速度为 3 实验及结果
10 m/s，最近距离为 10 m，最近点时间为 10 s。分
别在仿真的接收信号中加入高斯白噪声，SNR计算 3.1 实验
方法采用谱SNR。两种算法搜索结果对比如图 6 和 针对上述理论和仿真结果，进行实验。陆面目
表 1所示。 标采用某卡车运动过程中辐射的线谱噪声，数据来
从图 6 和表 1 中可以看出，在仿真条件相同的 源为 acousticstoday.org。该信号时长 30 s，采样频
情况下，SNR 过低时，Sevcik 维数和熵作为代价函 率为12000 Hz。声速为347 m/s。最近距离为35 m，
数效果均不佳，这是因为当 SNR 较低时，噪声对信 速度为 20 km/h。其到达最近点时间为 15.2 s，本文
号频谱有较大影响，因此两种方法均会失效。但是， 在处理过程中将其设为已知量。接收信号 LOFAR
从图 6 可以看出，Sevcik 维数作为代价函数抗噪性 图以及搜索结果如图8所示。
提高 5 dB 左右。主要原因是两种算法都基于频谱 图 8(a) 为接收器接收信号 LOFAR 图，该图中
的混乱程度，即使在 SNR 低于 −5 dB 的情况下，多 线谱多普勒十分明显。设置速度网格为[1 : 0.1 : 15]，
普勒的存在与否也会对频谱的 Sevcik 维数产生较 单 独 搜 索 速 度 的 结 果 如 图 8(b) 所 示， 结 果 为
大影响，即存在多普勒时频谱的 Sevcik 维数明显大 5.8 m/s，相对误差仅为 4.4%，该结果证明了本
于不存在时，因此本文算法可行。而只有在 SNR大 文算法的有效性。本文方法与熵值方法搜索结果对
于 −5 dB 以后，用熵值作为代价函数时，多普勒的 比如图 8(c)所示。计算两种算法速度搜索结果的主
存在与否对频谱的影响较大，熵值作为代价函数的 瓣宽度，熵值算法的主瓣宽度为3.15 m/s，本文算法
算法才会有效。SNR 对多普勒是否存在时两种不 的主瓣宽度仅为 0.74 m/s，结果表明本文算法主瓣
同代价函数的影响如图 7(a)、图 7(b) 所示。在相同 宽度明显更窄。