Page 64 - 《应用声学》2023年第6期

1174 2023 年 11 月

相邻两节点的传播时间t可表示为 心，最大步进距离为半径，范围内的所有节点即看
作与选定节点直接相连。最大步进距离影响了算法
t = d/v g , (13)
每一步中需要计算、比较和更新的节点数量，进而
其中，d 为两节点距离，v g 为两点间的群速度平均
同样影响计算效率。以节点平均间距 d = 0.2 mm
值。由于计算时相邻节点间距一般比较小，可以使
为单位，选取 n = 2d、n = 5d、n = 8d 和 n = 15d，
用两端节点处的群速度值代替平均值v g 。算法运行
计算与图5同样的声传播路径，结果如图6所示。可
完成后，得到区域内所有节点到指定起点的最短传
以看出，n = 2d时的计算结果与其他路径差异较大，
播时间。对每一个节点，通过逐级追踪父节点的方
式可以得到源点到节点的传播路径。 50
d/
图 4 为位于 (−20 mm, 50 mm) 处的点声源从 40 d/
d/⊲
一侧介质穿过焊缝区域，到达另一侧介质的传播路
径计算结果。可以看到，在进入焊缝区域前，介质为 z/mm 30
各向同性，声传播路径为直线；进入各向异性焊缝区 20
域后，声线发生扭曲和弯折，靠近焊缝中间区域弯折 10
最为明显；穿过焊缝区域后，恢复直线传播。
0
50 -40 -30 -20 -10 0 10 20 30 40
x/mm
40 (a) ࣱکᓬགᫎᡰd=2 mmnjd=1 mmnjd=0.5 mm

z/mm 30 50 d/⊲
20
40 d/⊲
d/⊲
10 30
z/mm
0
-40 -20 0 20 40 20
x/mm
10
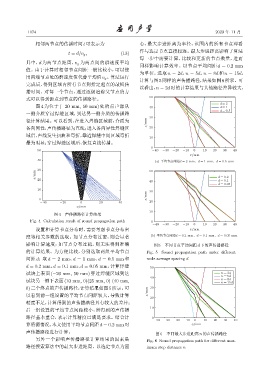
图 4 声传播路径计算结果
Fig. 4 Calculation result of sound propagation path 0
-40 -30 -20 -10 0 10 20 30 40
设置和计算节点分布时，需要考虑节点分布密 x/mm
度等相关参数的选取。如节点分布过密，则会显著 (b) ࣱکᓬགᫎᡰd=0.2 mmnjd=0.1 mmnjd=0.05 mm
影响计算速度；如节点分布过疏，则无法得到准确 图 5 不同节点平均间距 d 下的声传播路径
的计算结果。为方便比较，分别选取两组平均节点 Fig. 5 Sound propagation path under different
间距 d：取 d = 2 mm、d = 1 mm、d = 0.5 mm 和 node average spacing d
d = 0.2 mm、d = 0.1 mm、d = 0.05 mm，计算焊缝 50
试块上表面 (−20 mm, 50 mm) 穿过焊缝区域到达 n/d
40 n/d
试块另一侧下表面(10 mm, 0)(25 mm, 0) (40 mm, n/d
n/d
0)三个终点的声传播路径，计算结果如图5所示。可 30
以看到前一组设置的平均节点间距较大，导致计算 z/mm
20
精度不足，计算得到的声传播路径具有较大的差异；
后一组设置的平均节点间距较小，所得到的声传播 10
路径基本重合，表示计算精度已满足要求。结合计 0
-40 -30 -20 -10 0 10 20 30 40
算资源情况，本文使用平均节点间距d = 0.2 mm对 x/mm
声传播路径进行计算。 图 6 不同最大步进距离 n 的声传播路径
另外一个影响声传播路径计算结果的因素是 Fig. 6 Sound propagation path for different max-
路径搜索算法中的最大步进距离。以选定节点为圆 imum step distance n