Page 19 - 《应用声学》2024年第1期

第 43 卷 第 1 期 刘与涵等： 深海声影区时频谱干涉结构与声源定位 15

图 2 为声影区内频率干涉周期 ∆f 的值随水平 将式 (7) 代入式 (6)，得到频率 f 处的时间干涉
距离的变化曲线。由于∆f 随水平距离单调变化，该 周期∆t的表达式
特征量可用于声源距离估计。 c r
∆t ≈ . (8)
f · v r · [cos θ 1 (t) − cos θ 3 (t)]
z s =7 m, z r =200 m
30
图 3 为 200 Hz 频点处 ∆t 的值随水平距离的变
化曲线，其中v r =10 m/s。尽管式(8)中的cos θ 1 (t)−
20
Df/Hz cos θ 3 (t) 项导致 ∆t 与水平距离呈非单调关系，但在

10 距离已知的条件下可计算cos θ 1 (t) − cos θ 3 (t)的值，
从而估计声源的径向速度v r 。

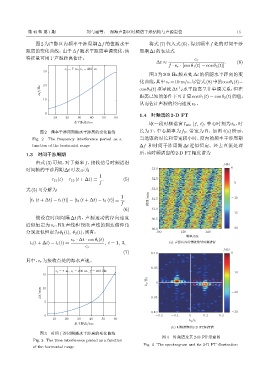
0 1.4 时频谱的2-D FT
10 20 30 40 50 60
ඵࣱᡰሏ/km
取一段时频谱窗 I win (f, t)，中心时刻为 t 0 ，时
图 2 频率干涉周期随水平距离的变化曲线 长为 T，中心频率为 f 0 ，带宽为 B。如图 4(a) 所示，
Fig. 2 The frequency interference period as a 当选取的时长和带宽较小时，窗内的频率干涉周期
function of the horizontal range ∆f 和时间干涉周期 ∆t 近似恒定。经去直流处理
1.3 时间干涉周期 后，该时频谱窗的2-D FT幅度谱为
由式 (3) 可知，对于频率 f，接收信号时频谱沿 /dB
时间轴的干涉周期∆t可表示为 33.0 0
1
τ 13 (t) − τ 13 (t + ∆t) ≡ . (5) 32.5
f -5
式(5)可分解为 32.0
1 31.5 -10
[t 1 (t + ∆t) − t 1 (t)] − [t 3 (t + ∆t) − t 3 (t)] ≡ . ௑ᫎ/min
f
(6) 31.0
-15
假设在时间间隔 ∆t 内，声源运动的径向速度 30.5
近似恒定为 v r ，BR 声线和 BSR 声线的到达俯仰角
30.0 -20
分别近似恒定为θ 1 (t), θ 3 (t)，则有： 100 120 140
ᮠဋ/Hz
v r · ∆t · cos θ i (t)
t i (t + ∆t) − t i (t) ≈ , i = 1, 3, (a) ܦॖӝЯᄊଌஆηՂ௑ᮠ៨ቔ
c r
/dB
(7) 0.10 0
其中，c r 为接收点处的海水声速。
0.05
z s=7 m, z r=200 m, f=200 Hz -10
15
k t /Hz 0

Dt/min 10 -0.05 -20

5

-0.10 -30
0 -0.2 -0.1 0 0.1 0.2
10 20 30 40 50 60
k f/s
ඵࣱᡰሏ/km
(b) ௑ᮠ៨ቔᄊ2-D FTࣨए៨
图 3 时间干涉周期随水平距离的变化曲线
图 4 时频谱及其 2-D FT 示意图
Fig. 3 The time interference period as a function
Fig. 4 The spectrogram and its 2-D FT illustration
of the horizontal range