Page 197 - 《应用声学》2024年第1期

第 43 卷 第 1 期 姚震等： 超声焊接全状态频率跟踪算法 193

2 全状态频率跟踪算法的推导与实现 不难看出，式 (7) 有 4 个解，由于负频率没有物

理意义，舍去两个负数解后可得
2.1 全状态频率跟踪算法的推导
 √
√ 2
假设当前电源输出频率为 f，角频率为 ω，其  1 −K 2 − K − 4K 1 K 3 ,
2

 f r =

 2π
对应的换能器两端电压电流相位差为 θ。由于相位 2K 1 (8)
√
√
2
差角度与负载阻抗角相同 [4] ，由式 (1) 可以推导出  1 −K 2 + K − 4K 1 K 3

2

 f a = .

tan θ 与ω 之间的关系为 2π 2K 1
[( )
1 1 当阻性点不存在时，目标频率计算公式如下：
tan θ = ωL 1 −
R 1 ωC 1 √
1
( ( ) )] −K 2 (9)
2
1 f = .
2
− ωC 0 R + ωL 1 − . (4) 2π 2K 1
1
ωC 1
在式(7)和式(8)中，ω 是当前的发波频率，tan θ
在式(4)的基础上进一步化简可以得到以下表达式：
则是换能器相位差的正切值，可选f a 或f r 作为目标
2
2
−C 0 L ω 3 2C 0 L 1 + C 1 L 1 − R C 1 C 0
1
1
tan θ = + ω 跟踪频率。因此，只要求出K 1 、K 2 、K 3 三个未知数，
R 1 R 1 C 1
即可同时得到换能器的谐振频率和反谐振频率。值
C 0 + C 1
− . (5) 2
R 1 C 1 ω 得注意的是，当K − 4K 1 K 3 < 0时，函数无实数解，
2
为使表达式变得简洁，现进行以下等效变换： 说明换能器此时不存在阻性点，其计算方式如式(9)

C 0 L 1 所示。

 K 1 = − ,


 R 1

 2.2 全状态频率跟踪算法的实现

2C 0 L 1 + C 1 L 1 − 2C 0 L 1
K 2 = , (6)
 R 1 C 1 依据 f r 和 f a 的计算公式 (式 (8))，可根据应用



 C 0 + C 1
 场合选择跟踪目标是 f r 还是 f a ，一般情况下 f r 用

 K 3 = − 2 .
R 1 C 1 于中小负载的工况，而 f a 则用于负载较大的情况。
把式(6)代入式(5)后等式两边同时乘ω，可得
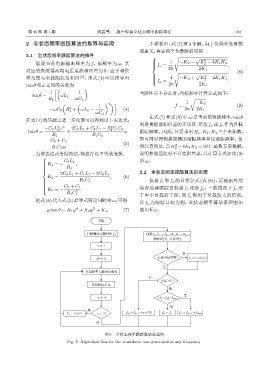
以 f a 为跟踪目标为例，全状态频率算法流程图如
4
2
ω tan θ = K 1 ω + K 2 ω + K 3 . (7) 图 5所示。
नݽ
ੳᮠᆸࠀቇᣒ௑ᄊ f a Ѿၹf n ֒f n֓ ֒f n֓ ֒θ n ֒θ n֓ ֒θ n֓
රᝍर(7), ᝠካѣf c
n/
ա
f c ௧ա௧ࠄ஝⋆ f c=real(f c↽
f n /f a
௧
̿ᝈᮠဋf n ᣥѣ̔ืႃ
ա
θ n  >θ l ⋆
᧔ನᄱͯࣀ θ n
௧
௧
n⇁⇁ f c ֓f n >f max
ա
௧
f n =f  +s n > ⋆ f n /f n֓ ⇁sSn̺ f n /f c f n /f n֓ ⇁f max
ա
图 5 全状态频率跟踪算法流程图
Fig. 5 Algorithm flow for the transducer was generated at any frequency