Page 215 - 《应用声学》2024年第1期

第 43 卷 第 1 期 段润泽等： 自由空间内悬挂气泡破碎时的声学特性 211

大，也就是说气流的扩散速度会随着气泡半径的增 的压力波动代入，将公式(17)修正为公式(19)：
大而增大，导致液膜边缘的速度振幅变大，从而导致 √ 2σρ 0 1
p a ≈ 2bc 0 kr 2 0 . (19)
气泡破碎时声发射的特征振幅增大。 r 0 r
公式 (15) 在计算气泡液膜边缘的速度振幅时， 将气泡的物性参数与气泡破碎时声发射过程
所用的气泡内外压强差为单位面积上的压力差，气 的特征频率代入公式 (19)，得到气泡大小与气泡破
泡受重力效应顶部逐渐减薄，产生初始破碎点，液膜 碎时声发射的特征频率之间的关系。以表面张力系
边缘受表面张力作用卷曲，初始破碎点逐渐发展，气 数为变量的实验结果与修正后的特征振幅公式对
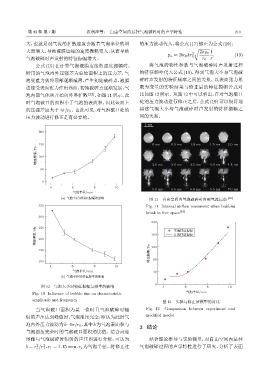
泡内部气体也开始向外界扩散 [22] ，如图 11所示，此 比如图12所示。从图 12中可以看出，在对气泡破口
时气泡破口的面积小于气泡的表面积，因此该面上 处的压力波动进行修正之后，公式 (19) 可以很好地
的压强差应大于4σ/r 0 。由此可见，对气泡破口处的 描述气泡大小与气泡破碎时声发射的特征振幅之
压力波动进行修正是有必要的。 间的关系。
1 cm
200

150 0 ms 0.5 ms 1.0 ms 1.5 ms 2.0 ms
ྲढ़૝ࣨ/Pa 100

50 2.5 ms 3.0 ms 3.5 ms 4.0 ms 4.5 ms

0
4 6 8 10
5.0 ms 5.5 ms 6.0 ms 6.5 ms 7.0 ms
ඡจӧय़/mm
(a) ඡจӧय़ࠫྲढ़૝ࣨᄊॖ־ 图 11 自由空间内气泡破碎时内部气流运动 [22]
350 Fig. 11 Internal airflow movement when bubbles
break in free space [22]
300
200
ྲढ़ᮠဋ/Hz 200 160 ࠄᰎྲढ़૝ࣨ
250
ᝠካྲढ़૝ࣨ

ྲढ़૝ࣨ/Pa
150 120

100 80
4 6 8 10
ඡจӧय़/mm 40
(b) ඡจӧय़ࠫྲढ़ᮠဋᄊॖ־
0
图 10 气泡大小对特征振幅与频率的影响 4 6 8 10
Fig. 10 Influence of bubble size on characteristic ඡจӧय़/mm
amplitude and frequency
图 12 实验与修正后模型的对比
当气泡破口面积为某一值时且气泡破碎时辐 Fig. 12 Comparison between experiment and
射的声压达到峰值时，气泡泄压完全，即认为此时气 modified model
泡内外压力波动为b · 4σ/r 0 ，其中b为气泡表面积与
3 结论
气泡泄压完全时的气泡破口面积的比值。结合高速
图像与气泡破碎时辐射的声压图进行分析，可认为 结合理论推导与实验测量，对自由空间内悬挂
2
b = r /r ，r 1 = 4.15 mm，r i 为气泡半径。将修正过 气泡破碎过程的声学特性进行了研究，分析了表面
2
i 1