Page 49 - 《应用声学》2024年第1期

第 43 卷 第 1 期 陈茁等： 波束开角对多普勒测频结果的影响 45

其中，
τ, (28)
U = M k 2 (0) cos 2πf d 0 τ + N k 2 (0) sin 2πf d 0
τ, (29)
V = N k 2 (0) cos 2πf d 0 τ − M k 2 (0) sin 2πf d 0
I
∑ [ ( f d ) ]
′
M = (S i 2 i 2 a ′ ) sin 2πi∆f 1 + τ , (30)
a − S −i 2 −i 2
f 0
i 2 =1
I
∑ [ ( f d ) ]
N = S i 2 (0) a ′ + ′ a ′ ) cos 2πi∆f 1 + τ , (31)
i 2 (0) (S i 2 i 2
a + S −i 2 −i 2
f 0
i 2 =1
′
P 1 = ((a ′ N −k 2 cos 2πdkτ + a N k 2 ) + a ′ M −k 2 sin 2πdkτ) cos 2πk∆ −1 τ, (32)
−k 2 k 2 −k 2
G 1 = ((a ′ M −k 2 cos 2πdkτ + a M k 2 ) − a ′ N −k 2 sin 2πdkτ) cos 2πk∆ −1 τ, (33)
′
−k 2 k 2 −k 2
P 2 = ((a ′ M −k 2 cos 2πdkτ − a M k 2 ) − a ′ N −k 2 sin 2πdkτ) sin 2πk∆ −1 τ, (34)
′
−k 2 k 2 −k 2
′
G 2 = ((a ′ N −k 2 cos 2πdkτ − a N k 2 ) + a ′ M −k 2 sin 2πdkτ) sin 2πk∆ −1 τ. (35)
−k 2 k 2 −k 2
忽略相关函数积分化简过程中引入的误差以 -1
͌ᄾϙ
及水底椭圆模型简化误差时，利用式 (27) 可计算波 Нरϙ
束开角导致的测频偏差。 -2
฾ᮠϠࣀ/Hz
3 仿真与试验数据分析 -3
3.1 仿真实验 -4
前文已经分析具有一定波束开角的水底椭圆
散射模型下回波信号测频偏差受到波束开角的影 -5
5 10 15 20
响。不同方位扩展损失、散射强度的差异导致频谱 ฉౌनᝈ/(°)
不对称，测频结果偏小，且随波束开角增大，频谱不
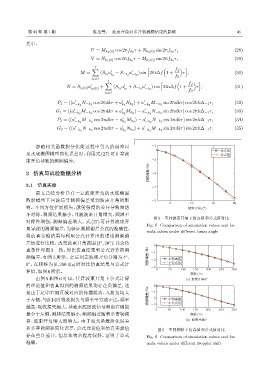
图 5 不同波束开角下仿真值和公式值对比
对称性增强，测频偏差增大。式 (27) 可计算波束开
Fig. 5 Comparison of simulation values and for-
角导致的测频偏差，为验证测频偏差公式的准确性，
mula values under different beam angle
将仿真实验结果与利用公式计算出的理论测频偏
差值进行比较。改变波束开角范围[2 , 20 ]，其余仿
◦
◦
0
真条件与图 3 一致，对比仿真结果和公式计算的测 -1
频偏差，如图 5 所示。之后固定波束开角分别为 4 、 ฾ᮠϠࣀ/Hz -2 4°͌ᄾϙ
◦
6 ，在频移为 [0, 300 Hz] 时对比仿真结果与公式计 4°Нरϙ
◦
-3
算值，如图6所示。 0 50 100 150 200 250 300
ᮠረ/Hz
由图 5 和图 6 可知，任意波束开角下公式计算 (a) ฉౌनᝈ4°
的理论值和仿真得到的测频结果均存在负偏差，这 0
是由于足印右侧区域对应的传播距离、入射角均大 ฾ᮠϠࣀ/Hz -1
于左侧，与此同时吸收损失与频率平方成正比，频率 -2 6°͌ᄾϙ
6°Нरϙ
越高，吸收损失越大，导致水底回波信号频谱右侧能 -3
0 50 100 150 200 250 300
量少于左侧，测频结果偏小，测频偏差随着多普勒频 ᮠረ/Hz
移、波束开角增大而增大。由于相关函数简化误差 (b) ฉౌनᝈ6°
和多普勒频移简化误差，公式理论值和仿真实验值 图 6 不同频移下仿真值和公式值对比
存在些许差异，但总体吻合程度较好，证明了公式 Fig. 6 Comparison of simulation values and for-
准确。 mula values under different Doppler shift