Page 194 - 《应用声学》2024年第6期

1370 2024 年 11 月

表 1所示。 形聚能器的前四阶弯曲振动模态振型图。
表 1 金属材料参数 为了方便比较，将理论计算与有限元仿真的聚
Table 1 Metal material parameters 能器的前四阶弯曲共振频率值列于表 2，其中 f t 表
示利用传递矩阵模型计算得到的共振频率，f c 表示
密度/ 杨氏模量/ 剪切模量/
材料
(kg·m −3 ) (N·m −2 ) (N·m −2 ) 有限元仿真计算出来的频率，∆ 1 表示理论与仿真计
45# 钢 7850 20.9×10 10 8.23×10 10 算结果的相对误差，其中∆ 1 = |f t − f c |/f c 。

复合楔形聚能器的各个部分尺寸参数分别为：
L 1 = 20 mm，L 2 = 30 mm，H 1 = W 1 = 10 mm， 10
H 2 = W 2 = 16 mm。当复合楔形聚能器的材料 5
及尺寸参数确定后，由式 (12) 可得如图 3 所示的聚 25733 Hz 50204 Hz
能器弯曲共振的频率响应曲线。由图 3 可知，在 ᛡѵरᄊϙ/10 14 0 71162 Hz 94411 Hz
0∼100 kHz 的频率范围内有 4 个值，分别对应于聚 -5
能器的一阶弯曲共振频率 25733 Hz、二阶弯曲共振 -10
频率50204 Hz、三阶弯曲共振频率71162 Hz和四阶
-15
弯曲共振频率94411 Hz。 20 40 60 80 100
ᮠဋ/kHz
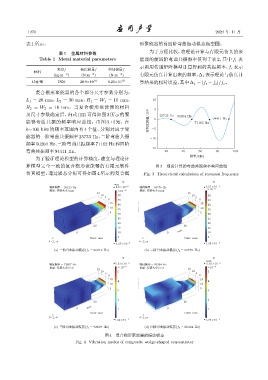
为了验证理论模型的计算精度，建立与理论计
算模型完全一致的复合楔形聚能器的有限元软件 图 3 理论计算的弯曲共振频率响应曲线
仿真模型，通过模态分析可得如图 4 所示的复合楔 Fig. 3 Theoretical calculation of resonant frequency

mm
ྲढ़ᮠဋ=25212 Hz 5.5T10 -5 ྲढ़ᮠဋ=50776 Hz 5.51T10 -5
T10 -6
᛫᭧: ͯረܸ࠵/mm T10 -6 ᛫᭧: ͯረܸ࠵/mm
15 15
10 50 10 50
5 5
0 45 0 45
15 15
40 40
10 10
35 35
5 5
30 30
25 25
20 20
20 20
15 15
mm
0 10 0 10
5 5
z Unit: mm z Unit: mm
y x y x
2.47T10 -7 1.39T10 -7
(a) ʷ᫽िజ૝үവগ(f  =25212 Hz) (b) ̄᫽िజ૝үവগ(f  =50776 Hz)
mm
ྲढ़ᮠဋ=72697 Hz 5.53T10 -5 ྲढ़ᮠဋ=95294 Hz 5.55T10 -5
᛫᭧: ͯረܸ࠵/mm T10 -5 ᛫᭧: ͯረܸ࠵/mm T10 -5
15 15
10 5 10 5
5 5
0 0
15 15
4 4
10 10
5 5
3 3
2 2
20 20
mm
0 1 0 1
Unit: mm Unit: mm
z z
y x y x
1.22T10 -7 3.74T10 -7
(c) ʼ᫽िజ૝үവগ(f  =72697 Hz) (d) پ᫽िజ૝үവগ(f  =95294 Hz)
图 4 复合楔形聚能器的振动模态
Fig. 4 Vibration modes of composite wedge-shaped concentrator