Page 195 - 《应用声学》2024年第6期

第 43 卷 第 6 期 文仕豪等： 弯曲振动复合楔形超声聚能器的设计 1371

表 2 理论数值与有限元数值对比 3 振动性能分析
Table 2 Comparison of theoretical and fi-
nite element method values 为了研究复合楔形聚能器的尺寸对聚能器的
弯曲共振频率 f 以及放大系数 M 的影响规律，定义
振动模态 f t/Hz f c/Hz ∆ 1 /%
一阶 25733 25212 2.06 N 为聚能器的后端长方体与前端楔形块大端的高
二阶 50204 50776 1.12
度比，即 N = (H 2 /H 1 )；定义 U 为聚能器的后端长
三阶 71162 72697 2.11 方体与前端楔形块的长度比，即 U = (L 2 /L 1 )。当
四阶 94411 95294 0.92
聚能器的楔形块的大段高度和长度固定后，通过改
由表 2 可以看出，理论计算值与有限元仿真值
变长方体的高度和长度，即可改变 N 和 U 的值，计
之间的相对误差在 0.92%∼2.06%之间，表明本文基
算可得不同高度比和长度比对聚能器各阶弯曲共
于 Timoshenko 弯曲梁理论推导的复合楔形聚能器
振频率和放大系数的影响特性。图 6 为理论计算与
共振频率方程具有较高的理论计算精度；并且在高
有限元仿真所得的聚能器的各阶弯曲共振频率与
阶振动模式下仍然具有很高的理论计算精度。
其高度比 N(蓝色线)和长度比U(红色线) 的变化关
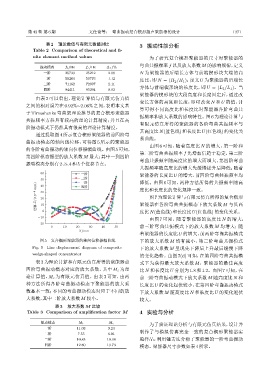
通过提取图 4所示复合楔形聚能器的前四阶弯
系曲线。
曲振动模态的轴向线位移，可得图 5 所示的聚能器
由图 6 可知，随着高度比 N 的增大，第一阶和
的各阶弯曲振动的轴向位移振幅曲线。由图5可知，
第三阶弯曲共振频率 f 先增加后趋于稳定，第二阶
第四阶模态振型的放大系数M 最大；其中一到四阶
弯曲共振频率随高度比的增大而增大，第四阶弯曲
振型模态分别有2、3、4和5个位移节点。
共振频率随高度比的增大先缓慢提升后降低；随着
60 ʷ᫽ 聚能器的长度比 U 的增大，前四阶弯曲共振频率均
50 ̄᫽ 降低。由图 6 可知，两种方法所得的共振频率随高
ʼ᫽
ͯረ Z/(10 -6 mm) 30 度比和长度比的变化规律一致。
40
پ᫽
图7为理论计算与有限元仿真所得的复合楔形
20
聚能器在各阶弯曲共振模态下放大系数 M 与其高
10

-10 0 度比N(蓝色线)和长度比U(红色线)的变化关系。
由图 7 可知，随着聚能器的高度比 N 的增大，
-20
0 10 20 30 40 50 前三阶弯曲共振模式下的放大系数 M 均增大；随
X/mm
着聚能器的长度比 U 的增大，前两阶弯曲共振模式
图 5 复合楔形聚能器的轴向位移振幅曲线 下的放大系数 M 均有减小，第三阶弯曲共振模式
Fig. 5 Line displacement diagram of composite 下的放大系数 M 呈现先下降后上升最后缓慢下降
wedge-shaped concentrator
的变化趋势。由图 7(d) 可知，在第四阶弯曲共振模
表3 为理论计算和有限元仿真所得的聚能器前 式下为获得最大放大系数 M，聚能器的最佳高度
四阶弯曲振动模态对应的放大系数，其中 M t 为理 比 N 和长度比 U 分别为 1.8 和 1.2。由图 7 可知，在
论计算值，M c 为有限元仿真值。由表 3 可知，由两 前三阶弯曲振动模式下放大系数 M 随高度比 N 和
种方法所得各阶弯曲振动模态下聚能器的放大系 长度比 U 的变化起伏较小，在第四阶弯曲振动模式
数基本一致；不同的弯曲振动模态对应于不同的放 下放大系数 M 随高度比 N 和长度比 U 的变化起伏
大系数，其中二阶放大系数M 较小。 较大。
表 3 放大系数 M 比较
Table 3 Comparison of amplification factor M 4 实验与分析

振动模态
为了验证理论分析与有限元仿真结果，设计并
M t
M c
一阶 11.03 9.24
二阶 7.55 6.01 制作了与模拟仿真完全一致的复合楔形聚能器实
三阶 10.85 10.08 验样品，利用锤击法分析了聚能器的一阶弯曲振动
四阶 12.60 13.73 模态。聚能器尺寸参数如表4所示。