Page 177 - 《应用声学》2025年第1期

第 44 卷 第 1 期 聂磊鑫等： 高斯过程辅助的船舶辐射噪声分类算法 173

它定义的线性算子相当于使 N t 阶单位阵中主 区域没有任何的先验，它可能选择很高复杂度的方
对角线上的第 v 个元素为 0；同时，H 2 表示对时频 式去拟合这些区域，这对泛化是不利的；mixup的数
谱图掩蔽集合Φ m 中包含的时间帧。 据扩增鼓励模型在无实测数据覆盖(也即需要泛化)
1.3 添加随机噪声操作 的区域学习线性插值函数，会有效降低学得的模型
在此区域的复杂度，进而有助于模型的泛化 [20] 。
添加随机噪声 H 3 (·) 将对时频分析前的声压
数据添加不同 SNR 的随机噪声，再进行短时傅里
2 数据扩增策略带来的边缘分布偏移分析
叶变换(Short Time fourier transformation, STFT)
¯ a
并取模得到增广时频谱图 S ；尽管 STFT是线性的 尽管在实际中每次对数据样本进行增广时选
i
变换，但由于添加固定功率的噪声和逐点取模的操 用的增广变换 H(·) 是从多个可能的变换中随机挑
作都不是线性的，所以 H 3 (·) 无法使用线性变换去 选的，但在此为方便对增广后数据分布的偏移进

明确写出。 行理论分析，假定每次增广均使用同一个变换。以
1.4 mixup操作 线性变换 H 1 (·) 或 H 2 (·) 为例，它们处理数据的值

除了这些具有物理含义的数据增广变换外，现 x i ，但通常不会改变 x i 所服从的分布 (也即数据 D
代深度学习中也使用一些进阶的数据增广技术，例 的边缘分布) 的类型，而只是使分布中的参数发生
如 mixup 数据增广 [20] ：它通过超参数 λ 对任意两 变动。若数据集合 D = {(x i , y i )} N 的边缘分布服
i=1
个随机的实测船舶噪声时频谱图数据进行线性插 从均值向量为 µ，协方差矩阵为 C 的多元高斯分布
值，这相当于混合了这两个时频谱图图像，相应的 N(µ, C)，即
船舶类别以独热 (One-Hot)编码的形式写为软标签 1
p(x) = √
N
后，也以相同的超参数进行混合；扩增变换 H 4 (·) 可 (2π) det C
( 1 )
表示为 × exp − (x − µ) C −1 (x − µ) , (7)
T
2

 ¯ a ¯ ¯ −1
S = λS i + (1 − λ)S j ,
(6) 其中，det C 和 C 分别计算了协方差矩阵 C 的
 a 行列式和逆。线性变换 H 1 作用后的数据 D =
y = λy i + (1 − λ)y j ,
a
¯
¯
其中，λ ∈ [0, 1]服从贝塔分布；而(S i , y i )和(S j , y j ) {(H 1 x i , y i )} N 的边缘分布仍服从高斯分布，但均
i=1
T
均为训练中可得的实测数据，通过对分帧后的所有 值变为H 1 µ，协方差矩阵变为H 1 ΣH ；这使得D a
1
训练数据进行不放回抽样并对其中声压信号进行 与D具有显然不同的边缘分布。
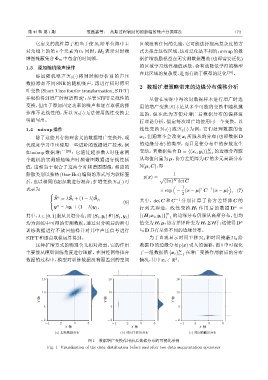
STFT和逐点取模运算得到。 为了直观显示时间平移 H 1 和时间掩蔽 H 2 给
这种扩增方式的物理含义相对薄弱，它的作用 数据 D 的边缘分布 p(x) 引入的偏移，图1 中可视化
主要能从模型训练角度进行理解。在神经网络拟合 了一组数据值 {x i } N 在增广变换作用前后的分布
i=1
2
数据的过程中，模型对训练数据没有覆盖到的空间 情况，其中x i ∈ R 。
16 16 16

10 10 10
Y ᣉ Y ᣉ Y ᣉ
4 4 4

-2 -2 -2
-1 2 5 8 -1 2 5 8 -1 2 5 8
X ᣉ X ᣉ X ᣉ
(a) Ԕݽ஝૶Ѭ࣋ (b) ௑ࣱᫎረՑѬ࣋ (c) ௑ᫎଏᘉՑѬ࣋
图 1 数据增广变换作用前后数据分布的可视化示例
Fig. 1 Visualization of the data distribution before and after two data augmentation operators