Page 172 - 《应用声学》2025年第1期

168 2025 年 1 月

估计值相对平稳，但是2D-MUSIC 方法受搜索间隔 法具有更好的估计性能，湖上试验数据的处理结果
的影响，导致估计角度存在误差，且估计时间长。由 验证了该方法在实际场景下的实用性。
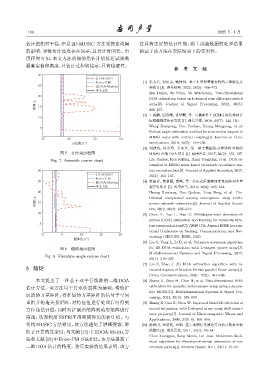
历程图可知，本文方法的俯仰角估计值接近试验数
据真实俯仰角度，且估计过程较稳定，具有稳健性。
参 考 文 献
30
2D-MUSIC
Euler-PM [1] 朱大君, 何培宇, 喻伟闯. 基于 L 型和差嵌套阵的二维波达方
25 EDOA-Matrix 向估计 [J]. 信号处理, 2022, 38(3): 466–473.
వ஡வข
Zhu Dajun, He Peiyu, Yu Weichuang. Two-dimensional
20
DOA estimation based on L-shaped sum difference nested
௑ᫎ/s 15 array[J]. Journal of Signal Processing, 2022, 38(3):
466–473.
[2] 王咸鹏, 国月皓, 黄梦醒, 等. 互耦条件下 MIMO 雷达非圆目
10
标稳健角度估计方法 [J]. 通信学报, 2019, 40(7): 144–150.
Wang Xianpeng, Guo Yuehao, Huang Mengxing, et al.
5
Robust angle estimation method for noncircular targets in
MIMO radar with mutual coupling[J]. Journal on Com-
15 20 25 30
வͯᝈ/̵°̶ munications, 2019, 40(7): 144–150.
[3] 刘建涛, 任岁玲, 姜永兴, 等. 基于数据协方差矩阵重构的
图 7 方位角历程图 MIMO 声纳 DOA 估计 [J]. 应用声学, 2017, 36(2): 162–167.
Fig. 7 Azimuth course chart Liu Jiantao, Ren Suiling, Jiang Yongxing, et al. DOA es-
timation in MIMO sonar based on sample covariance ma-
30 trix reconstruction[J]. Journal of Applied Acoustics, 2017,
2D-MUSIC 36(2): 162–167.
Euler-PM
25 EDOA-Matrix [4] 黄惠祥, 郭秋涵, 童峰, 等. 分布式压缩感知麦克风阵列多声
వ஡வข 源方位估计 [J]. 应用声学, 2019, 38(4): 605–614.
20 Huang Huixiang, Guo Qiuhan, Tong Feng, et al. Dis-
௑ᫎ/s 15 tributed compressed sensing microphone array multi-
source azimuth estimation[J]. Journal of Applied Acous-
tics, 2019, 38(4): 605–614.
10
[5] Chen Y, Yan L, Han C. Millidegree-level direction-of-
arrival (DOA) estimation and tracking for terahertz wire-
5
less communications[C]//2020 17th Annual IEEE Interna-
tional Conference on Sensing, Communication, and Net-
0 5 10 15 20 working (SECON). IEEE, 2020.
ο̈́ᝈ/̵°̶
[6] Liu S, Yang L, Li D, et al. Subspace extension algorithm
图 8 俯仰角历程图 for 2D DOA estimation with L-shaped sparse array[J].
Multidimensional Systems and Signal Processing, 2017,
Fig. 8 Elevation angle course chart
28(1): 315–327.
[7] Liu S, Zhao J. 2D DOA estimation algorithm with in-
5 结论 creased degrees of freedom for two parallel linear arrays[J].
China Communications, 2020. 17(6): 101–108.
本文提出了一种基于双平行线阵的二维 DOA [8] Zhang X, Zhou M, Chen H, et al. Two-dimensional DOA
估计方法。该方法以平行水听器阵为基础，构造扩 estimation for acoustic vector-sensor array using a succes-
sive MUSIC[J]. Multidimensional Systems & Signal Pro-
展的协方差矩阵，将扩展协方差矩阵的信号子空间
cessing, 2014, 25(3): 583–600.
重组并构造关系矩阵，对特征值进行处理后可得到 [9] Zhang X, Gao X, Chen W. Improved blind 2D-direction of
方位角估计值，同时对扩展后的阵列流形矩阵进行 arrival estimation with L-shaped array using shift invari-
ance property[J]. Journal of Electromagnetic Waves and
筛选，从而利用 ESPRIT 得到俯仰角的估计值。与
Applications, 2009, 23(5–6): 593–606.
传统 MUSIC 方法相比，该方法避免了谱峰搜索，降 [10] 陈相国, 宋爱民, 刘剑. 基于非圆信号波达方向估计的最大似
低了计算的复杂度；与文献[15]中EDOA-Matrix方 然算法 [J]. 现代雷达, 2011, 33(1): 51–54.
Chen Xiangguo, Song Aimin, Liu Jian. Maximum likeli-
法和文献[15]中Euler-PM方法相比，该方法提高了
hood algorithm for direction-of-arrival estimation of non
二维DOA估计的精度。仿真实验的结果表明，该方 circulars signals[J]. Modern Radar, 2011, 33(1): 51–54.