Page 170 - 《应用声学》2025年第1期

166 2025 年 1 月

步骤 6 根据角度关系，由式 (19)、式 (25) 计算 70
出方位角φ k 的估计值 ˆφ k 。
60 60.5
60.0
2.4 克拉美罗界(CRB) 59.5
30
在 本 节 中， 通 过 两 个 平 行 线 性 阵 列 推 导 50
2D-DOA 估计的克拉美罗界 (Cramer-Rao bound, ο̈́ᝈ/̵°̶ 2D-MUSIC
CRB)，整个数组的方向矩阵为 A ∈ C 4(M−1)×K ， 40 45.5 Euler-PM
定义为 45.0 EDOA-Matrix
30 44.5 వ஡வข
  10 11 ᄾࠄᝈए
A y1 Ω H
 
20
 
 A y1  0 10 20 30 40 50 60
A =   = [a r1 , a r2 , · · · , a rK ] . (28)
  வͯᝈ/̵°̶
 A y1 Ω 
 
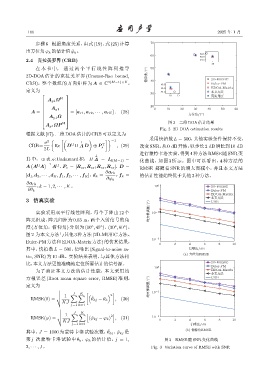
H 图 2 二维 DOA 估计结果
A y1 ΩP
Fig. 2 2D DOA estimation results
根据文献[17]，二维DOA估计的CRB可以定义为
采用快拍数 L = 500，其他实验条件保持不变，
−1
[(
)
]}
{
σ 2 H ⊥ T
CRB= Re D Π A D ⊕ P s , (29) 改变 SNR，从0 dB 开始，以步长 2 dB 增长到 10 dB
2L
进行蒙特卡洛实验，得到 4种方法 RMSE随SNR变
⊥
其 中，⊕ 表 示 Hadamard 积，Π A = I 4(M−1) − 化曲线，如图 3 所示。图中可以看出，4 种方法的
( H ) −1 H
A A A A ，P s = [R ss , R ss ; R ss , R ss ]，D = RMSE 都随着 SNR 的增大而减小，并且本文方法
∂a rk
[d 1 , d 2 , · · · , d K , f 1 , f 2 , · · · , f K ]，d k = ，f k = 的估计性能始终优于其他3种方法。
∂φ k
∂a rk
，k = 1, 2, · · · , K。 10 0 2D-MUSIC
∂θ k Euler-PM
EDOA-Matrix
వ஡வข
3 仿真实验 CRB
实验采用双平行线性阵列，每个子阵由 12 个 کவಪឨࣀ/(°) 10 -1
阵元组成，阵元间距为 0.03 m，两个入射信号的角
度 (方位角，俯仰角) 分别为 (10 , 45 )、(30 , 60 )。
◦
◦
◦
◦
图 2 为本文方法与其他 3 种方法 (2D-MUSIC 方法、
10 -2
Euler-PM 方法和 EDOA-Matrix 方法) 的仿真结果，
0 2 4 6 8 10
其中，快拍数 L = 500，信噪比 (Signal-to-noise ra- η٪උ/dB
tio, SNR) 为 10 dB。实验结果表明，与其他方法相 (a) வͯᝈRMSE
比，本文方法更能准确地定位所要估计的信号源。 2D-MUSIC
10 0 Euler-PM
为了验证本文方法的估计性能，本文采用均 EDOA-Matrix
వ஡வข
方根误差 (Root mean square error, RMSE) 准则， CRB
定义为 کவಪឨࣀ/(°)
v -1
u J K [ ] 10
u 1 ∑ ∑ ( ) 2
ˆ
RMSE(θ) = t θ kj − θ k , (30)
KJ
j=1 k=1
v
u J K
u 1 ∑ ∑ [ 2 ] -2
RMSE(φ) = t ( ˆφ kj − φ k ) , (31) 10 0 2 4 6 8 10
KJ
j=1 k=1 η٪උ/dB
ˆ
其中，J = 1000 为蒙特卡洛试验次数，θ kj 、ˆφ kj 是 (b) ο̈́ᝈRMSE
第 j 次蒙特卡洛试验中 θ k 、φ k 的估计值，j = 1, 图 3 RMSE 随 SNR 变化曲线
2, · · · , J。 Fig. 3 Variation curve of RMSE with SNR