Page 171 - 《应用声学》2025年第1期

第 44 卷 第 1 期 王绪虎等： 平行线阵扩展协方差矩阵二维波达方向估计方法 167

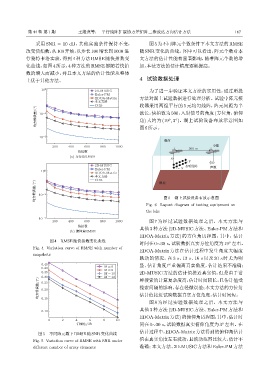
采用 SNR = 10 dB，其他实验条件保持不变， 图5 为不同阵元个数条件下本文方法的RMSE
改变快拍数，从100开始，以步长100增长到1000 进 随 SNR变化的曲线。图中可以看出，阵元个数对本
行蒙特卡洛实验，得到 4 种方法 RMSE 随快拍数变 文方法的估计性能有显著影响，随着阵元个数的增
化曲线，如图 4 所示，4 种方法的 RMSE 都随着快拍 加，本法方法的估计精度逐渐提高。
数的增大而减小，并且本文方法的估计性能从整体
上优于其他方法。 4 试验数据处理
10 0 2D-MUSIC 为了进一步验证本文方法的实用性，通过所提
Euler-PM
EDOA-Matrix 方法对湖上试验数据进行处理分析。试验中阵元接
వ஡வข
CRB 收器采用两组平行的 5 元均匀线阵，阵元间距为半
کவಪឨࣀ/(°) 10 -1 波长，快拍数为 500，入射信号的角度 (方位角，俯仰

角) 大约为 (19 , 3 )。湖上试验设备布放示意图如
◦
◦
图6所示。
10 -2
ຬ᭧
࠵ᓕ
200 400 600 800 1000
300 m
ঌથ஝
(a) வͯᝈRMSE
Z
Y
2D-MUSIC ඵզ٨᫼ ܦູ
Euler-PM X
10 0
EDOA-Matrix
వ஡வข
CRB ຬअ
کவಪឨࣀ/(°) 10 -1 图 6 湖上试验设备布放示意图

Fig. 6 Layout diagram of testing equipment on
the lake
10 -2
200 400 600 800 1000 图 7 为经过试验数据处理之后，本文方法与
ঌથ஝
其他 3 种方法 (2D-MUSIC 方法、Euler-PM 方法和
(b) ο̈́ᝈRMSE
EDOA-Matrix 方法) 的方位角历程图，其中，估计
图 4 RMSE 随快拍数变化曲线
时间在0∼30 s，试验数据真实方位角度为 19 左右。
◦
Fig. 4 Variation curve of RMSE with number of
EDOA-Matrix 方法在估计过程中发生角度大幅度
snapshots
跳动的情况，在 3 s、13 s、16 s 以及 20 s 时尤为明
0.45 显，估计角度严重偏离真实角度，估计结果不准确；
0.40 M/
M/
0.35 2D-MUSIC 方法的估计值接近真实值，但是由于谱
M/
0.30 M/ 峰搜索的计算复杂度高，估计时间较长，且估计值受
کவಪឨࣀ/(°) 0.20 搜索间隔的影响，存在轻微误差；本文方法的方位角
0.25
估计值接近试验数据真实方位角度，估计时间短。
0.15
图 8 为经过实验数据处理之后，本文方法与
其他 3 种方法 (2D-MUSIC 方法、Euler-PM 方法和
0.10
EDOA-Matrix方法)的俯仰角历程图，其中，估计时
0 2 4 6 8 10
◦
η٪උ/dB 间在 0∼30 s，试验数据真实俯仰角度为 3 左右。在
估计过程中，EDOA-Matrix方法得到的俯仰角估计
图 5 不同阵元数下 RMSE 随 SNR 变化曲线
Fig. 5 Variation curve of RMSE with SNR under 值在真实角度左右波动，且波动范围比较大，估计不
different number of array elements 准确；本文方法、2D-MUSIC 方法和 Euler-PM 方法