Page 207 - 《应用声学》2025年第2期

第 44 卷 第 2 期 高江俊康等： 粒子群优化算法下的多声速剖面声线计算 467

在Bellhop得到的结果中，2 条声线的出射角度 速函数重新设置，使其在水平方向上分段，将声速剖
从下至上分别为 15.7279 和 −15.8092 ；本文程序 面在水平方向上的梯度离散为若干声速剖面区间，
◦
◦
计算得到的 2 条声线角度从下至上分别为 15.8772 ◦ 以模拟真实海况下声速剖面的分布情况。对于声速
和15.9512 ，平均误差为0.924%。 在深度和距离方向均存在梯度的情况：
◦
c (z, r) = c 0 + g z z + g r r, (7)
0
其中，c 0 为声源处的声速，g z 、g r 分别为声速在垂直
100
和水平方向上的梯度。为了得到声线方程，寻求亥
200 姆霍兹方程如下形式的解：
ງए/m p (z, r) = e iωτ(z,r) ∑ A j (z, r) (8)
∞
300
(iω) j ,
j=0
400 其中，ω 为声源的角频率。可以推导出程函方程为
1
2
|∇τ| = . (9)
500 2
1500 1520 1540 1560 1580 c (z, r)
ܦᤴ/(mSs -1 ) 按以下微分方程定义声线轨迹：
(a) ᠇೙एܦᤴҖ᭧ dx
= c∇τ, (10)
0 ds
BELLHOPፇ౧
వ஡ሮऀፇ౧ 参数s为沿射线方向的弧长。则程函方程可以写作：
100 1 dx 1
∇τ · = , (11)
c ds c 2
200 即
ງए/m dτ 1
300
ds = c . (12)
时延计算的积分公式可表示为
400
∫ s 1
′
T = ds . (13)
′
500 0 c (s )
0 2000 4000 6000 8000 10000
ᡰሏ/m 模型中将声源与接收点之间水域沿着水平距
(b) Bellhopขˁవ஡ካขᄊᝠካፇ౧ࠫඋ 离平均分为 m 段，每段具有各自不同的声速剖面。
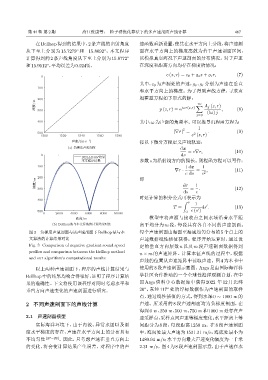
图 3 负梯度声速剖面与该声速剖面下 Bellhop 法与本 每个声速剖面由海面至海底均匀分布的 5 个点上的
文算法的计算结果对比 声速数据线性插值获得。程序开始运算时，通过设
Fig. 3 Comparison of negative gradient sound speed 定的垂直方向层数 n 以及 m 段声速剖面数据得到
profiles and comparison between the Bellhop method
n × m 的声速矩阵。计算本征声线的过程中，根据
and our algorithm’s computational results
声线的位置从声速矩阵中读取声速。图 4 为本节中
以上两种声速剖面下，程序的声线计算结果与 使用的8段声速剖面示意图。Argo是由国际海洋科
Bellhop中的结果均吻合得很好，证明了程序计算结 学社区合作推动的一个全球性海洋观测计划，在中
果的准确性。下文将使用该程序对同时考虑水平和 国 Argo 资料中心数据库中获得 2022 年 12 月北纬
◦
◦
垂直方向声速变化的声速剖面进行研究。 20 、东经 117 处的浮标数据作为声速剖面的取样
点，通过线性插值的方式，得到水深 0 ∼ 1000 m 的
2 不同声速剖面下的声线计算 声速。所采用的 8 段声速剖面均为负梯度剖面，在
海深0 m、250 m、500 m、750 m 和1000 m处存在声
2.1 声速剖面模型 速采样点，采样点间声速等梯度变化；水平距离上等
实际海洋环境下，由于内波、异常水团以及温 间距分为 8 段，每段距离 1250 m。在 8 段声速剖面
度水平梯度的存在，声速在水平方向上的分布具有 中，海面处最大声速为 1531.31 m/s，海底处最小为
不均匀性 [27−29] 。因此，只考虑声速在垂直方向上 1480.94 m/s；水平方向最大声速变化幅度为一千米
的变化，将会使计算结果产生误差。对程序中的声 2.31 m/s。图4 为8 段声速剖面示意，由于声速在水