Page 209 - 《应用声学》2025年第2期

第 44 卷 第 2 期 高江俊康等： 粒子群优化算法下的多声速剖面声线计算 469

0 0

200 200

ງए/m 400 ງए/m 400

600 600

800 800

1000 1000
0 2000 4000 6000 8000 10000 0 2000 4000 6000 8000 10000
ᡰሏ/m ᡰሏ/m
(a) ঽ኎ܦᤴҖ᭧ʾܦጳڏ (b) ӭ඀ܦᤴҖ᭧ʾܦጳڏ
0 0

200 200

ງए/m 400 ງए/m 400

600 600

800 800

1000 1000
0 2000 4000 6000 8000 10000 0 2000 4000 6000 8000 10000
ᡰሏ/m ᡰሏ/m
(c) 4඀ܦᤴҖ᭧ʾܦጳڏ (d) 8඀ܦᤴҖ᭧ʾܦጳڏ
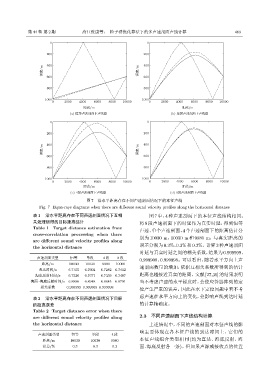
图 7 沿水平距离存在不同声速剖面情况下的本征声线
Fig. 7 Eigen-rays diagrams when there are different sound velocity profiles along the horizontal distance
表 1 沿水平距离存在不同声速剖面情况下互相 图 7 中，4 种声速剖面下的本征声线结构相同。
关处理所得的目标距离估计 将 8 段声速剖面下的时延作为真实时延，得到恒等
Table 1 Target distance estimation from
声速、单个声速剖面、4 个声速剖面下的距离估计分
cross-correlation processing when there
别为 10030 m、10030 m 和 9980 m，与真实距离的
are different sound velocity profiles along
误差分别为0.3%、0.3%和0.2%。计算 3种声速剖面
the horizontal distance
时延与真实时延之间的相关系数，结果为 0.999999、
声速剖面类型 恒等 单段 4 段 8 段
0.999908、0.999998。可以看出，随着水平方向上声
距离/m 10030 10030 9980 10000
速剖面数量的增加，依据互相关系数所得到的估计
直达时间/s 6.7155 6.7602 6.7282 6.7432
海底反射时间/s 6.7226 6.7677 6.7339 6.7487 距离也越接近真实的距离。文献[27,30]的结果表明
海面 -海底反射时间/s 6.8896 6.8948 6.8645 6.8791 当不考虑声速的水平梯度时，会使应答器阵列的定
相关系数 0.999999 0.999908 0.999998
位产生严重的误差。因此在水下定位问题中若不考
虑声速在水平方向上的变化，会影响声线到达时延
表 2 沿水平距离存在不同声速剖面情况下目标
的距离误差 的计算精确度。
Table 2 Target distance error when there
are different sound velocity profiles along 2.3 不同声速剖面下声线结构计算
the horizontal distance 上述情况中，不同的声速剖面对本征声线的影
响主要体现在各本征声线的到达时间上，它们的
声速剖面类型 恒等 单段 4 段
距离/m 10030 10030 9980 本征声线组合类型相同 (均为直达、海底反射、海
误差/% 0.3 0.3 0.2 面 -海底反射各一条)。但如果声源或接收点的位置