Page 57 - 《应用声学》2025年第2期

第 44 卷 第 2 期 杨雨等： 微通道内声传播格子 Boltzmann 建模及其特性研究 317

度解析解的最高峰值为 5.33 × 10 −3 ，不论是衰减趋 图 5 显示了 800 个时间步后的二维和三维声压
势还是速度分布，LBM解和理论解都非常吻合。 分布图。模拟区域的左边界设置声源，并沿 x 轴移
动。当声波传播到达刚性壁表面时，大部分声波
6
ᝍౢᝍ 被反射，产生传播波和反射波的干涉，形成了驻波
͌ᄾᝍ (x = 33处的固壁)，此时声压幅值有明显的“爬坡”
4
ඵࣱᤴए/(10 -3 luSts -1 ) 2 0 N y Ԧु ࢻڍܞ ܱ଎᣸ႍ
y

᣸ႍ
-2
ࣱ
Ԧ
᭧ n m ௄
࠱
-4 ฉ ᣸
ູ ႍ
-6
0 100 200 300 400 500 600 700 800 900 1000
ඵࣱಫག/lu ܱ଎᣸ႍ x
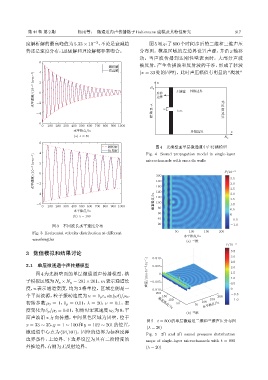
(a) λ=50 N x
6
ᝍౢᝍ 图 4 光滑壁面单层微通道中声传播模型
͌ᄾᝍ
4 Fig. 4 Sound propagation model in single-layer
ඵࣱᤴए/(10 -3 luSts -1 ) 2 0 200 P/10 3.5
microchannels with smooth walls

-3

180
-2
160
2.5
140 3.0
-4 120 2.0
ۇᄰಫག/lu 100 1.5
-6 1.0
0 100 200 300 400 500 600 700 800 900 1000 80
ඵࣱಫག/lu 0.5
60 0
(b) λ=100
40 -0.5
20 -1.0
图 3 不同波长水平速度分布
Fig. 3 Horizontal velocity distribution at different 50 100 150 200
ඵࣱಫག/lu
wavelengths (a) ̄፥
P/10 -3
3 数值模拟和结果讨论 3.5
3.0
0.010
3.1 单层微通道中声传播模型 0.005 2.5
2.0
图 4 为光滑壁面的单层微通道声传播模型，格 ܦԍ/(muSts -2 Slu -1 ) 0 1.5
子模拟区域为N x × N y = 201 × 201。m表示通道长 -0.005 1.0
0.5
度，n 表示通道宽度，均为 2 格单位。区域左侧是一 -0.010 0
200
个平面波源，粒子振动速度为 u = δ ρ c s sin(ωt)/ρ 0 ， 150 200 -0.5
100 150 -1.0
初始参数 ρ 0 = 1，δ ρ = 0.01，λ = 20，ν = 0.1，密 ۇᄰಫག/lu 50 50 100
ඵࣱಫག/lu
度变化为δ ρ /ρ 0 = 0.01。初始时宏观速度u 0 为0，平
(b) ʼ፥
面声波沿 x 方向传播，中间黑色区域为固壁，位于
图 5 t = 800 的单层微通道二维和三维声压分布图
x = 33 ∼ 35、y = 1 ∼ 100和y = 102 ∼ 201的位置，
(λ = 20)
微通道中心点为 (34,101)。固壁的边界为标准反弹
Fig. 5 2D and 3D sound pressure distribution
边界条件，上边界、下边界设置为具有二阶精度的 maps of single-layer microchannels with t = 800
外推边界，右侧为无反射边界。 (λ = 20)