Page 61 - 《应用声学》2025年第2期

第 44 卷 第 2 期 杨雨等： 微通道内声传播格子 Boltzmann 建模及其特性研究 321

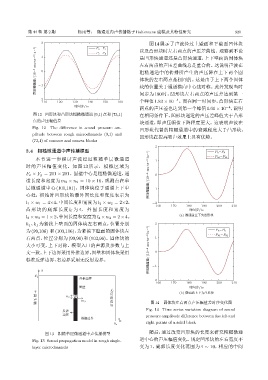
2 1 P o֓P s 以及凸形块时左右两点的声压差曲线。观察到不论
图 14 展示了声波经过上壁面和下壁面凹体块
ܦԍࣨϙࣀ/(10 -3 muSts -2 Slu -1 ) -1 0 是凹形块通道还是凸形块通道，上下壁面的固体块
P c֓P f
左右两点的声压差曲线总是重合的。这说明声波在
粗糙通道中的传播所产生的声压降在上下两个固
体块的左右两点是相同的。这是由于上下两个固体

间步为 180 时，凹形块左右两点的声压差达到第一
-2 块的位置关于通道横向中心线对称。此外发现当时
−4
110 120 130 140 150 160 个峰值 1.83 × 10 。而在同一时间步，凸形块左右
௑ᫎ൦/ts −4
两点的声压差也达到第一个峰值 1.61 × 10 ，说明
图 12 凹形块和凸形块粗糙微通道 (9,1) 点和 (73,1) 在相同条件下，凹形块通道的声压差峰值大于凸形
点的声压幅值差 块通道，即声压幅值下降程度更大。这表明声波在
Fig. 12 The difference in sound pressure am-
凹形块代替的粗糙通道中的衰减程度大于凸形块，
plitude between rough microchannels (9,1) and
凹形块在提高吸声效果上具有优势。
(73,1) of concave and convex blocks
2
3.4 粗糙微通道中声传播模型 P h ֓P k
本节进一步探讨声波经过粗糙单层微通道 1 P h֓P k
时的声压幅值变化。如图 13 所示，模拟区域为
F x × F y = 201 × 201。固壁中心是粗糙微通道，通 ܦԍࣨϙࣀ/(10 -4 muSts -2 Slu -1 ) 0
道长度和宽度为 m 3 × n 3 = 10 × 10，观测点在单
层微通道中心 (101,101)。固体块位于通道上下中 -1
心处，初始时凹形块的最外围长度和宽度表示为
l 1 × w 1 = 4×4，中间长度和宽度为 l 2 × w 2 = 2×2， -2
160 170 180 190 200 210
凸形块的底部长度 l 5 为 4， 外围长度和宽度为 ௑ᫎ൦/ts
l 3 × w 3 = 1 × 2，中间长度和宽度为l 4 × w 4 = 2 × 4。 (a) ॲᤰ᥋ʽʾ˞Ѣॎڱ
h 1 、k 1 为紧挨上壁面的固体块左右两点，位置分别 2
为(99,106) 和 (103,106)，为紧挨下壁面的固体块左 P h ֓P k
右两点，位置分别为 (99,96) 和 (103,96)。固体块的 1 P h ֓P k
大小可变，上下对称。模型入口的声源及参数与上
文一致，上下边界采用外推边界，固壁和固体块采用 ܦԍࣨϙࣀ/(10 -4 muSts -2 Slu -1 ) 0
标准反弹边界，右边界采用无反射边界。

y -1
F y
ܱ଎᣸ႍ
-2
160 170 180 190 200 210
ڍܞ ௑ᫎ൦/ts
௄
ࣱ (b) ॲᤰ᥋ʽʾ˞ѡॎڱ
᭧ n  h  k Ԧ
ܦ h k ࠱
m  ᣸
ູ 图 14 固体块左右两点声压幅值差时序变化图
ႍ
Fig. 14 Time series variation diagram of sound
Ԧु
᣸ႍ pressure amplitude difference between the left and
ܱ଎᣸ႍ x
right points of a solid block
F x
图 13 粗糙单层微通道中声传播模型 随后，通过改变凹形块的长度来研究粗糙微通
Fig. 13 Sound propagation model in rough single- 道中心的声压幅值变化。规定凹形块的左右宽度不
layer microchannels 变为 1，底部长度变化范围为 4 ∼ 10，相应的中间