Page 58 - 《应用声学》2025年第2期

318 2025 年 3 月

现象，说明当声波遇到固体壁面时，声压幅值逐渐增 固壁和右固壁之间的区域传播，并与右固壁反射过
加，形成一种声压波腹，就像声波爬升到更高的声压 来的声波叠加形成驻波，剩余的声波经过右通道发
幅值水平。另外一部分声波会穿过微通道，在固壁 生声波衍射现象，此时的声能能量经过不断的反射、
另一侧继续传播。结果发现，经过微通道的声压幅 吸收后逐渐减弱。
值明显下降，这是由于声波在遇到固体媒介时，界面
200 P/10 -3
特性阻抗骤变，声波在微通道内产生多次反射，消 4
180
耗了大部分能量，所以穿过微通道的声能量会变弱， 160 3
2
声压幅值水平骤减，壁面右侧区域呈现声波衍射的 140 1
现象。 ۇᄰಫག/lu 120 0
100
3.2 双层微通道中声传播模型 80 -1
-2
60 -3
双层微通道中声传播LBM模型如图6所示。模
40 -4
拟区域为 E x × E y = 201 × 201，左固壁的横坐标 20 -5
中心为 x 1 ，右固壁的横坐标中心为 x 2 。初始时左固 50 100 150 200
壁位于 x = 33 ∼ 43、y = 1 ∼ 96 和 y = 106 ∼ 201 ඵࣱಫག/lu
的位置，右固壁位于 x = 100 ∼ 110、y = 1 ∼ 96 和
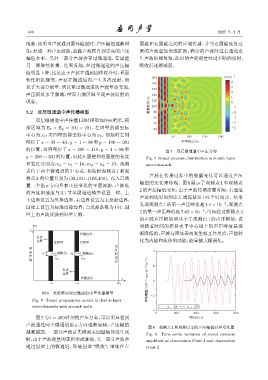
图 7 双层微通道中声压分布
y = 106 ∼ 201的位置，因此左固壁和右固壁的长度 Fig. 7 Sound pressure distribution in double-layer
和宽度分别为 m 1 = n 1 = 10、m 2 = n 2 = 10。观测 microchannels
点位于两个微通道的中心点，初始时观测点 1 和观
声波在传播过程中的能量变化可以通过声压
测点2 的位置分别为(38,101)、(105,101)。在入口放
幅值的变化来体现。图 8 展示了观测点 1 和观测点
置一个沿 x 方向具有正弦变化的平面波源，声源处
2 的声压幅值变化，由于声波传播需要时间，右通道
的密度和速度与 3.1 节单层通道模型设置一样。上
声波到达时间约比左通道延迟 115 个时间步。结果
下边界设置为外推边界，右边界设置为无反射边界，
发现观测点1的第一声压峰值是3.4 × 10 −3 ，观测点
固壁上设置为标准反弹边界，当反弹系数为1 时，固
2的第一声压峰值是7.62 × 10 −4 ，可知经过观测点2
壁上的声波反弹到固壁左侧。
的声波声压幅值明显小于观测点 1 的声压幅值，说
y 明随着时间的推移水平中心线上的声压峰值是逐
E y 渐降低的，声波与固体表面发生相互作用后，声能转
ܱ଎᣸ႍ
Ԧु
᣸ႍ ࢻڍܞ Կڍܞ 化为内能和流体的动能，能量被大幅弱化。
௄
ࣱ Ԧ
᭧ ᜺฾ག 4
n  n  ᜺฾ག ࠱
ܦ ᣸
ູ m  m  ႍ
Ԧु 2
᣸ႍ
ܱ଎᣸ႍ x ܦԍࣨϙ/(10 -3 muSts -2 Slu -1 )
x  x  E x 0

图 6 光滑壁面双层微通道中声传播模型 -2
Fig. 6 Sound propagation model in double-layer
microchannels with smooth walls x=38 x=105
-4
0 100 200 300 400
图7 为t = 400时刻的声压分布，可以明显看到 ௑ᫎ൦/ts
声波通过两个微通道沿 x 方向逐渐衰减，声压幅值
图 8 观测点 1 和观测点 2 的声压幅值时序变化图
越来越弱。一部分声波首先碰到左固壁随即发生反
Fig. 8 Time series variation of sound pressure
射，由于声波能量的累积形成驻波，另一部分声波会 amplitude at observation Point 1 and observation
通过固壁上的微通道，即被固壁 “吸收”，继续在左 Point 2