Page 59 - 《应用声学》2025年第2期

第 44 卷 第 2 期 杨雨等： 微通道内声传播格子 Boltzmann 建模及其特性研究 319

通道间的距离也会影响声波传播，因此本文分 通过构建光滑壁面单/双层微通道中声传播
别调整固壁 1 和固壁 2 的位置，研究间距对声衰减 LBM 模型，能够清晰地模拟声波在微通道内的传
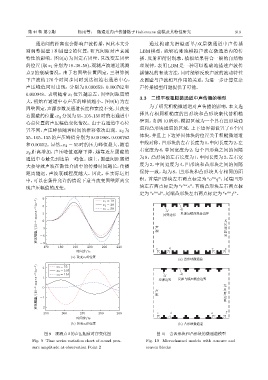
特性的影响。图 9(a) 为固定右固壁，只改变左固壁 播、反射和衍射现象，模拟结果符合一般的自然物
的位置(取x 1 分别为18、38、58)，观测声波通过观测 理规律，表明 LBM 是一种可以准确地描述声波传
点 2 的衰减情况。由于右固壁位置固定，三种算例 播情况的有效方法，同时能够反映声波的波动特性
下声波约 170 个时间步同时到达初始右通道中心， 及固壁与声波相互作用的关系，为进一步计算复杂
声压峰值同时出现，分别为 0.000653，0.000762 和 声传播模型问题提供了可能。
0.000948。表明随着 x 1 位置越靠左，固壁间距离增
3.3 二维平板粗糙微通道中声传播的模型
大，初始右通道中心声压的峰值越小。图 9(b) 为左
为了研究粗糙微通道对声传播的影响，本文选
固壁固定，声源参数及通道长度和宽度不变，只改变
择具有相同粗糙度的凹形块和凸形块来代替粗糙
右固壁的位置，x 2 分别为55、105、155时的右通道中
壁面。如图 10 所示，模拟区域为一个具有凹形块通
心点位置的声压幅值变化情况。由于右通道中心位
置不同，声压峰值随着时间的推移依次出现。x 2 为 道和凸形块通道的区域，上下边界都设置了 6 个固
体块，并且上下边界固体块的位置关于粗糙微通道
55、105、155 的声压峰值分别为 0.001868、0.000762
和0.00052。显然，x 2 = 55 时的压力峰值最大，随着 中线对称。凹形块的左右长度为1，中间长度为2，左
x 2 距离增加，声压峰值逐渐下降，越靠近左固壁的 右宽度为 4，中间宽度为 2，每个凹形块之间的间隔
通道中心最先到达第一峰值。综上，固壁间距离增 为8。凸形块的左右长度为1，中间长度为 2，左右宽
大会导致声波在黏性介质中的传播时间越长，传播 度为 2，中间宽度为 4，凹形块和凸形块之间的间隔
距离越远，声波衰减程度越大。因此，在实际运用 保持一致，均为 8。凹形块和凸形块具有相同的面
中，可以在条件允许的情况下适当改变固壁距离实 积。首端凹形块左右两点标定为 “o”“q”，尾端凹形
现声压幅值的改变。 块左右两点标定为 “r”“s”，首端凸形块左右两点标
定为“c”“d”，尾端凸形块左右两点标定为“e”“f”。
9
ܦԍࣨϙ/(10 -4 muSts -2 Slu -1 ) -3 3 0 x =58 ܦ Ԧु᣸ႍ Ԧुˁ᪫᭧ຉՌ᣸ႍ ௄
x =18
x =38

6
Ԧ
࠱
ູ
᣸
-6
-9
170 180 190 200 210 220 q ႍ
o r s
௑ᫎ൦/ts
(a) ஈԫx  ᄊͯᎶ
(a) Ѣॎڱॲᤰ᥋
ܦԍࣨϙ/(10 -3 muSts -2 Slu -1 ) -1 1 0 x  =155 ܦ Ԧु᣸ႍ Ԧुˁ᪫᭧ຉՌ᣸ႍ ௄
x  =55
2

x  =105

Ԧ
࠱
ູ
᣸
-2
250 260 270 280 290 c d e ႍ f
௑ᫎ൦/ts
(b) ஈԫx  ᄊͯᎶ (b) ѡॎڱॲᤰ᥋

图 9 观测点 2 的声压幅值时序变化图 图 10 含凹形块和凸形块的微通道模型
Fig. 9 Time series variation chart of sound pres- Fig. 10 Microchannel models with concave and
sure amplitude at observation Point 2 convex blocks