Page 139 - 《应用声学》2025年第3期

第 44 卷 第 3 期 修明明等： 一种基于虚元内插法的矢量互质阵测向干扰抑制方法 673

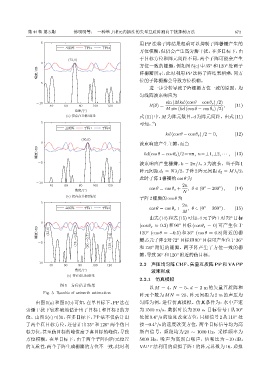
5 用 PP 法将子阵结果相乘可以抑制子阵栅瓣产生的
̉᠏᫼ ߕ᫼1 ߕ᫼2
方位模糊，但仍会产生高旁瓣干扰。在多目标下，由
于目标方位和阵元间距不同，两个子阵可能会产生
(72,0)
0 方位一致的栅瓣，例如图 5(c) 中 35 和 120 处两子
◦
◦
ࣨए/dB 阵栅瓣所示，此时利用 PP 法将子阵结果相乘，同方
位的子阵栅瓣会导致方位模糊。
-5
进一步分析导致子阵栅瓣方位一致的原因。均
匀线阵波束响应为
-10 sin (Mkd (cos θ − cos θ s ) /2)
40 60 80 100 120 B(θ) = , (11)
M sin (kd (cos θ − cos θ s ) /2)
ᝈए/(°)
(a) ̩ߛښᄬಖ1ፇ౧ 式(11) 中，M 为阵元数目，d 为阵元间距。由式 (11)
5
可知，当
̉᠏᫼ ߕ᫼1 ߕ᫼2
kd (cos θ − cos θ s ) /2 = 0, (12)
(90,0)
0 波束响应产生主瓣，而当
ࣨए/dB kd(cos θ − cos θ s )/2=nπ, n=±1, ±2, · · · , (13)

-5 波束响应产生栅瓣，k = 2π/λ，λ 为波长。当子阵 1
阵元间距 d 1 = Nλ/2，子阵 2 阵元间距 d 2 = Mλ/2，
此时子阵1栅瓣的cos θ 为
-10
40 60 80 100 120 2n
cos θ = cos θ s + , θ ∈ (0 − 360 ) , (14)
◦
◦
ᝈए/(°) N
(b) ̩ߛښᄬಖ2ፇ౧
子阵2栅瓣的cos θ 为
5
2n
̉᠏᫼ ߕ᫼1 ߕ᫼2 cos θ = cos θ s + , θ ∈ (0 − 360 ) . (15)
◦
◦
M
由式(14)和式(15) 可知，4 元子阵1 对72 目标
◦
0
(cos θ s ≈ 0.3) 和 90 目标 (cos θ s = 0) 可产生位于
◦
ࣨए/dB (35,0) 120 (cos θ = −0.5) 和 36 (cos θ ≈ 0.8) 附近的栅
◦
◦
◦
◦
-5 (73,-0.8) (90,-0.7) (120,-0.4) 瓣；5元子阵2对72 目标和90 目标可产生位于36 ◦
和 120 附近的栅瓣。两子阵产生了方位一致的栅
◦
瓣，导致36 和120 附近的伪目标。
◦
◦
-10
40 60 80 100 120 2.2 声压均匀阵 CBF、矢量互质阵 PP 和 VAPP
ᝈए/(°) 波束形成
(c) ߛښԥᄬಖፇ౧
2.2.1 仿真模拟
图 5 方位估计结果
以 M = 4、N = 5、d = 2 m 的矢量互质阵和
Fig. 5 Results of azimuth estimation
阵元个数为 MN = 20、阵元间距为 2 m 的声压均
由图 5(a) 和图 5(b)可知，在单目标下，PP 法在 匀阵为例，进行仿真模拟。仿真条件为：水中声速
旁瓣干扰下较准确地估计出了目标 1 和目标 2 的方 为 1500 m/s，数据时长为 200 s，目标信号 1 从 30 ◦
位。由图 5(c) 可知，在多目标下，PP 法不仅估计出 处按 0.4 /s 的速度改变方位，目标信号 2 从 110 处
◦
◦
了两个真目标方位，还估计出 35 和 120 两个伪目 按 −0.4 /s 的速度改变方位，两个目标信号均为高
◦
◦
◦
标方位，甚至伪目标的峰值高于真目标的峰值，导致 斯白信号，频段均为 20 ∼ 1000 Hz，采样频率为
方位模糊。在单目标下，由于两个子阵间阵元位置 5000 Hz，噪声为高斯白噪声，信噪比为 −10 dB。
的互质性，两个子阵生成栅瓣的方位不一致，此时利 VAPP 法利用的虚拟子阵 1 的阵元总数为 16，虚拟