Page 250 - 《应用声学》2025年第3期

784 2025 年 5 月

3
ρ m =1129 kg/m ，杨氏模量 E m = 5.3 GPa，剪切模 式 (17) 中，1 表示沿着纤维的长轴方向，2 和 3 位于
量G m = 2.0 GPa [20] 。 和纤维垂直的平面内；柔度矩阵中的各分量分别为
10 S 11 = 1/E 11 , S 22 = 1/E 22 , S 12 = −ν 12 /E 11 ,

8 S 12 = S 13 , S 33 = S 22 , S 23 = −ν 23 /E 22 ,
V ph /(kmSs -1 ) 6 4 S 44 = 1/G 23 , S 55 = 1/G 12 , S 66 = S 55 . (18)

根据柔度矩阵的对称性可写出柔度矩阵 S ij ，

2 Legendre 刚度矩阵与柔度矩阵互为倒数关系，
−1
′
Disperse C = S ij . (19)
ij
0
0 2 4 6 8 10 在计算柔度矩阵过程中，选取的坐标系沿着纤
f/MHz
维的轴向为主轴方向，在计算横观各向复合材料圆
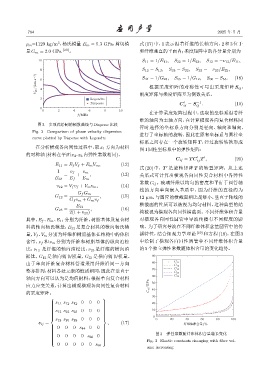
图 2 多项式绘制的频散曲线与 Disperse 比较
管时选择的坐标系方向分别是径向、轴向和轴向，
Fig. 2 Comparison of phase velocity dispersion
进行了坐标轴的旋转，因此在原有坐标系与圆柱坐
curve plotted by Disperse with Legendre
标系之间存在一个旋转矩阵 T ，经过旋转转换形成
在分析横观各向同性过程中，取x 1 方向为材料 图 1圆柱坐标系中的弹性矩阵：
的对称轴(材料在平面x 2 -x 3 内弹性常数相同)，
′
′
C ij = T C T , (20)
ij
E 11 = E f V f + E m V m , (12)
式 (20) 中，T 是旋转矩阵 T 的转置矩阵，从上述
′
1 v f v m
= + , (13) 关系式可计算出横观各向同性复合材料中各弹性
E 22 E f E m
常数 C ij 。玻璃纤维以均匀的密度和平行于圆管轴
v 12 = V f v f + V m v m , (14)
线的方向单向嵌入基质中，因为纤维的直径约为
G f G m
G 12 = , (15) 12 µm，与圆管的横截面相比足够小，垂直于轴线的
G f v m + G m v f
横截面的性质可以被视为均匀材料，这种典型的结
E 22
G 23 = , (16)
2(1 + v 23 ) 构被视为横观各向同性横截面。不同纤维体积含量
其中，E f 、E m 、E 11 分别为纤维、树脂基体及复合材 对横观各向同性圆管中导波传播有不同程度的影
料的轴向杨氏模量，E 22 是复合材料的横向杨氏模 响。为了研究导波在不同纤维体积含量圆管中的传
量，V f 、V m 分别为纤维和树脂基体在结构中的体积 播特性，结合细观力学理论 [19] 和方程 (18)，在图 3
含量，ν f 和 ν m 分别为纤维和树脂基体的纵向泊松 中绘制了横观各向同性圆管中不同纤维体积含量
比，ν 12 是纤维的轴向泊松比，ν 23 是纤维的横向泊 的5个独立弹性常数随体积含量的变化趋势。
松比，G 12 是轴向剪切模量，G 23 是横向剪切模量。 90
由于单向纤维复合材料管道采用纤维沿同一方向 80 C 
C 
整齐排列，材料各处元素的性质相同，因此在垂直于 70 C 
C 
轴向方向可以认为是均值材料；根据单向复合材料 60 C 
应力应变关系，计算出横观横观各向同性复合材料 C ij/GPa 50
的柔度矩阵： 40
30
 
 s 11 s 12 s 12 0 0 20

 0 
 
 
  10
 s 12 s 22 s 23 0 0 

 0 

 
  0
 
 s 12 s 23 s 22 0 0 0  0 20 40 60 80 100
s ij = , (17) ጜ፥ʹሥե᧚/%
 0 0 0 s 44 0 0 


 
 
 
  图 3 弹性常数随纤维体积含量增长变化
 0 0 0 0 s 66 0 


 
 
  Fig. 3 Elastic constants changing with fiber vol-
 
0 0 0 0 0 s 66
ume increasing