Page 106 - 201805
P. 106

688                                                                                  2018 年 9 月


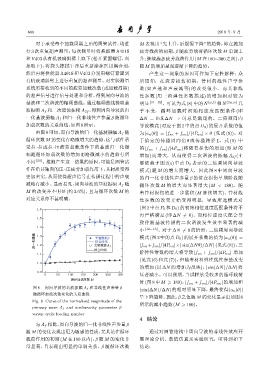
                 对于承受每个加载周期之后的圆管试件，均进                          M 表现出 “先上升，后缓慢下降” 的趋势，即在施加
             行 3 次重复超声测量；每次测量时将换能器 A401S                       疲劳载荷的初期，β 随疲劳载荷循环次数 M 单调上
             和 V403 从有机玻璃斜劈上取下 (松开紧固螺钉，直                       升；继续施加疲劳载荷作用 (M 在180∼300之间)，β
             接取下)，将探头擦拭干净后重新涂抹医用耦合剂，                           随M 的增加呈现逐渐下降的趋势。
             然后再将换能器 A401S 和 V403 分别用螺钉紧固到                         产生这一现象的原因可作如下定性解释：众
             有机玻璃斜劈上进行重复的超声测量。对实验测量                            所周知，在疲劳损伤初期，管材的线性声学参
             系统所接收到的不同的疲劳加载次数(或加载周期)                           数 (如声速和声衰减等) 的改变很小，而其非线
             的超声信号进行信号处理和分析，得到周向导波的                            性参数 (用三阶弹性常数描述) 的增加相对较为
             基波和二次谐波的幅频曲线。通过幅频曲线提取基                            明显   [31−32] ，可认为式 (8) 中的 N   (ω,l)  和 N (2ω,n)  几
             波振幅 A f 和二次谐波振幅A 2f ，得到周向导波的归                     乎不变， 循环加载时初始相速度匹配条件 (即
             一化基波振幅 A f 和归一化非线性声参量 β 随循环                       ∆N = 0 或 ∆N → 0) 总是满足的。二倍频周向
             加载次数的关系曲线，如图8所示。                                  导波模式 (对应于图 2 中的点 D 0 ) 的展开系数的值
                 由图8可知，周向导波的归一化基波振幅A f 随                       为 |a n (θ)| = |f sn + f vn |/|4P nn | × θ (见式 (9))。对
             循环次数M 的变化有略微增大的趋势，这与试件承                           于给定的传播周向角 θ 或传播路径 L，式 (9) 中
             受拉 -拉或拉 -压疲劳加载条件下的基波归一化振                          的 |f sn + f vn |/|4P nn | 将随着损伤的增加 (即 M 的
             幅随循环加载次数的增加而略微减小的趋势有所                             增加) 而增大，从而使得二次谐波的振幅 A 2f (主
             不同  [30] 。推测产生这一结果的原因，可能是圆管试                      要依赖于图 2(a) 中点 D 0 表示的二倍频周向导波
             件在沿其轴向的压-压疲劳加载作用下，其材质变得                           模式) 随 M 的增大而增大，因此图 8 中周向导波
             更加密实，从而使得超声信号在传播过程中的声衰                            的归一化非线性声参量 β 的值在损伤早期阶段随
             减略有减小。显而易见，周向导波的基波振幅A f 随                         循环次数 M 的增大而显著增大 (M < 180)。随
             M 的改变并不明显 (约 3.6%)，且与循环次数 M 的                     着管材损伤的进一步累积 (M 继续增大)，管材线
             对应关系亦不甚明确。                                        性参数的改变开始变得明显，导致所选模式对

                                                               (图 2 中点 P 0 和 D 0 ) 的初始相位速度匹配条件将不
                 1.6
                                                               再严格满足 (即 ∆N ̸= 0)，而相位速度失配会导
                 1.5
                                                               致伴随基波传播的二次谐波发生效率显著的减
                 1.4
                                                               小 [12−13] 。对于 ∆N ̸= 0 的情形，二倍频周向导波
                ॆʷӑࣨϙ  1.3                 ࠄᰎ஝૶β               模式 (图 2 中的点 D 0 ) 的展开系数的值为 |a n (θ)| =
                                           લՌజጳ
                                                               |f sn +f vn |/|4P nn |×| sin(∆Nθ)/∆N| (见式(8))。三
                 1.2
                                           ࠄᰎ஝૶A f
                                           લՌజጳ                阶弹性常数的增大将导致 |f sn + f vn |/|4P nn | 增加
                 1.1
                                                               (见式 (6) 和式 (7))，但随着材料弹性线性参量改变
                 1.0
                                                               的增加 (以 ∆N 的增加为反映)，| sin(∆N)/∆N| 将
                 0.9
                     0    50   100   150  200   250  300       显著减小。可以预期，当试样承受较多的循环载荷
                                 ॰ဗҫᣒ൓஝ M
                                                               时 (图 8 中 M > 180)，|f sn + f vn |/|4P nn | 的增加和
                图 8  周向导波的基波振幅 A f 和非线性声参量 β
                                                               | sin(∆N)/∆N| 的相对明显下降，最终使得 |a n (θ)|
                随循环加载次数变化的关系曲线
                                                               呈下降趋势。因此，β 之值随M 的变化显示出如图 8
               Fig. 8 Curve of the normalized magnitude of the
                                                               所示的减小趋势(M > 180)。
               primary wave A f and nonlinearity parameter β
               versus cyclic loading number
                                                               4 结论
                 与A f 相比，周向导波的归一化非线性声参量β
             随M 的变化表现出更为敏感的性质，尤其是在循环                               通过对圆管结构中周向导波的非线性效应开
             载荷作用的初期 (M 在 180 以内)，β 随 M 的变化非                   展理论分析、数值仿真及实验研究，可得到如下
             常显著，且表现出明显的单调关系。β 随循环次数                           结论：
   101   102   103   104   105   106   107   108   109   110   111