Page 215 - 201805

第 37 卷 第 5 期 宋云红等： 各向异性联合反演的数值研究 797

地层的快横波方位为X 轴方向，慢横波方位为 由式(7)可知，当θ = 45 时，XX、Y Y 分别为
◦
Y 。下面用遍历的方式观察主函数、辅助函数、综合 
 XX(t) = [S(t − s 1 z) + S(t − s 2 z)]/2,
函数以及各向异性大小随快慢横波慢度差和快横 (8)
 Y Y (t) = [S(t − s 1 z) + S(t − s 2 z)]/2.
波方位的变化趋势。
◦
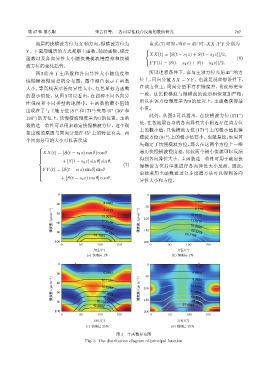
图 3 给出了主函数和各向异性大小随角度和 所以理想条件下，在与主轴方位夹角 45 的方
快慢横波慢度差的分布图。图中颜色表示主函数 位上，同向分量 XX = Y Y 。也就是说理想条件下，
大小，等高线表示各向异性大小，红色星标为函数 在该方位上，同向分量不存在慢度差，且波形完全
的最小值处。从图 3 可以看出，在四种不同各向异 一致。这比快横波与慢横波的波形相似更加严格，
性强度和不同类型的地层中，主函数的最小值均 所以在该方位慢度差为 0 的位置上，主函数获得最
小值。
出现在了与主轴方位 (81 和 171 ) 夹角 45 (36 和
◦
◦
◦
◦
此外，从图 3 可以看出，在快横波方位 (171 )
◦
126 ) 的方位上，快慢横波慢度差为 0 的位置。主函
◦
处，在各地层自身的各向异性大小附近存在该方位
数的这一特性可以用来确定快慢横波方位。这个现
上的极小值，且快横波方位 (171 ) 上的极小值比慢
◦
象出现的原因与同向分量在 45 上的特征有关。两
◦
横波方位 (81 ) 上的极小值要小。也就是说，如果首
◦
个同向分量的大小可以表示成
先确定了快慢横波方位，那么在这两个方位上一维

XX(t) = [S(t − s 1 z) cos θ] cos θ 遍历快慢横波慢度差，比较两个极小值就可以反演



 得到各向异性大小。主函数这一特性可用于确定快

+ [S(t − s 2 z) sin θ] sin θ,

(7) 慢横波方位后单独进行各向异性大小反演。因此，
Y Y (t) = [S(t − s 1 z) sin θ] sin θ


 单独采用主函数通过分步反演方法可以得到各向


 + [S(t − s 2 z) cos θ] cos θ.
异性大小和方位。
0 0
20 4.4562 3.388
50 6.776
ਥएࣀ/(µsSm -1 ) 60 13.3685 ਥएࣀ/(µsSm -1 ) 100 10.1639
8.9123
40
13.5519
17.8246
16.9399
22.2808
80
20.3279
31.1931 26.737 150 23.7158
100 200
0 50 100 150 0 50 100 150
வͯ/(°) வͯ/(°)
(a) ঌڡࡏ 1% (b) ਥڡࡏ 1%
0 0
20 6.0665 4.4914
50 8.9828
ਥएࣀ/(µsSm -1 ) 40 18.1994 ਥएࣀ/(µsSm -1 ) 100 13.4742
12.1329
60
17.9656
24.2658
30.3323
80 36.3987 150 22.4571
26.9485
31.4399
42.4652
100 200
0 50 100 150 0 50 100 150
வͯ/(°) வͯ/(°)
(c) ঌڡࡏ 25% (d) ਥڡࡏ 25%
图 3 主函数分布图
Fig. 3 The distribution diagram of principal function