Page 75 - 201805

第 37 卷 第 5 期 蔡飞燕等： 声操控微粒研究进展 657

[
1 1 2 1 示声场的强弱，微粒受到的声辐射力可以用射线理
F = − Re(α m ) ∇ |p| − Re(α d ) ρ∇|v| 2
2 2ρc 2 2 论来计算 [12] 。如图1所示，在声线法中，声辐射力由
k k 两部分组成，一部分是沿着声波传播方向的散射力，
( 4 )
+ Im(α m ) − Re(α m )Re(α d ) Re(pv )
∗
c 12πc
] 它由声波的反射引起，大小正比于声强；另一部分是
+ ρIm(α d )Im(v · ∇)v ∗ , (7) 梯度力，它的传播方向为声强梯度方向，与声场的能
其中，p 和 v 是一阶声压和速度场，ρ 是基体密 量梯度有关，指向声场强度最大处。声射线算法简
度，k = 2πf/c，Re 和 Im 分别表示场的实部和 单，计算速度快，但仅限于物体的尺寸远大于波长的
虚部，∗ 表示共轭，α m = α /[1 + i(k /4π)α ]、 情况。
0
0
3
m
m
3
0
α d = α /[1 − i(k /12π)α ] 分别表示球的单极子和 2.4 数值方法计算声辐射力
0
d d
偶极子模型对应的声场强度参量。其中， 对于复杂声场环境，不规则形状物体在声场中
 
4 ρc 2 受到的声辐射力无法用上述解析方法计算，因此人
0
3 

α = πa 1 − ) , (8)
m ( 们发展了多种数值方法计算声辐射力，如离散格子
3 2 4 2
ρ p c − c
l t
3 玻尔兹曼法 [13] 、有限体积法以及时域有限差分方
( ρ p − ρ )
0
α = 4πa 3 , (9) 法 [14] 。其中离散格子玻尔兹曼法仅能适用于极低
d
2ρ p + ρ
马赫数情况，限制了其在可压缩流动模拟中的应用。
其中，c l 、c t 和 ρ p 分别表示球的纵波速度、横波速度
有限体积法适合计算流体介质中的力，但缺点是计
和密度。在式 (7) 中，大括号内前面两项表示梯度
算精度不高，仅能处理波长远小于物体尺寸时的受
力，后面两项表示散射力。因此从式(7) 能够更直观
地体现声场的分布对力的方向和大小的影响。 力。时域有限差分方法是通过差分时空离散波动方
程，不借助任何模型直接获得全空间声场的实时演
2.3 微粒尺寸远大于波长的受力计算方法
化，结合微粒周围的动量张量表达，即可获得微粒受
当微粒的尺寸远大于声波的波长时，只考虑声 到的声辐射力。该方法是处理任意声场中复杂介质
波的粒子性而忽略波动性，可以用声线的疏密来表 声辐射力的非常有用的工具，但对于三维情况，其计
Y ूएѬ࣋ 算量较大需要高性能并行计算。
 F g Z
3 声操控微粒研究最新进展
a b
F a
声操控微粒研究工作在最近 20 年获得了广泛
O F s
的关注。在 Web of Science 以 “acoustic radiation
F b
a
b force” 和 “manipulation” 作为主题关键词，搜索到
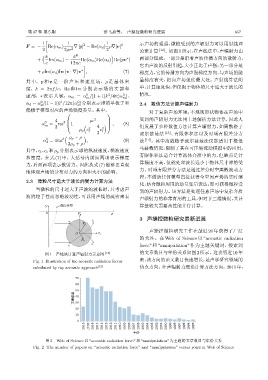
图 1 声线法计算声辐射力示意图 [12] 的文章数目与年份关系如图2所示。这表明近10年
Fig. 1 Illustration of the acoustic radiation forces 来，该方向的论文数目快速增长，是声学研究领域的
calculated by ray acoustic approach [12] 热点方向。在声辐射力理论计算方法方面：2011年，
70
60
50
஡ቦ஝ᄬ 40
30
20
10
0
2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996 1994 1992
2018 2017
ࣲ͋
图 2 Web of Science 以 “acoustic radiation force” 和 “manipulation” 为主题的文章数目与年份关系
Fig. 2 The number of papers on “acoustic radiation force” and “manipulation” versus years in Web of Science