Page 130 - 201901

126 2019 年 1 月

由质量定律可知，增加单一材质壳体的壁厚来 结构场接触面的声压级之差进行计算，同时根据
提高隔声量并不是一种高效的手段，在第 2.1 节针 式 (8) 给出数值计算结果，并将两者计算结果进行
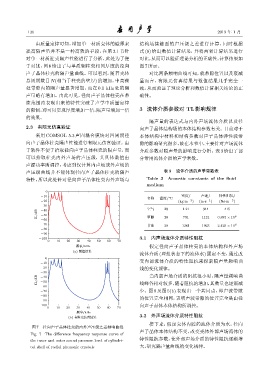
对单一材质柱壳隔声性能进行了分析，此处为了便 对比，从而可以验证理论分析的正确性，计算结果如
于对比，图 6 给出了与单质钢柱壳相同厚度的径向 图 7所示。
声子晶体柱壳的隔声量曲线。可以看到，随着壳体 对比两条频响曲线可知，就带隙位置以及衰减
总周期数目 N(相当于柱壳的壁厚) 的增加，中高频 量而言，有限元仿真结果与数值结果几乎完全一
处带隙内的隔声量显著增加，而在 0.1 kHz 处的隔 致，从而验证了理论分析和数值计算相关结论的正
声量略有增加。由此可见，径向声子晶体柱壳在带 确性。
隙范围内表现出来的特性突破了声学中质量定律
的限制，即可以实现厚度增加一倍，隔声量增加一倍 3 流体介质参数对 TL影响规律
的效果。
隔声量的表达式与内外声场流体介质以及径
2.3 有限元仿真验证 向声子晶体结构场的本体结构参数有关。目前对于

采用 COMSOL 5.3 声固耦合模块对四周期径 本体结构中材料和结构参数对声子晶体弹性波带
向声子晶体柱壳隔声性能进行有限元仿真验证。由 隙的影响研究很多，故在本节中，主要针对声场流体
于软件不便于拾取径向声子晶体柱壳的隔声量，而 介质参数对隔声量的影响进行分析。表 3 给出了部
可以拾取柱壳内外声场的声压级，其具体数值由 分常用流体介质的声学常数。
声源功率所调控，考虑到仅计算内声场或外声场的
声压级曲线并不能体现径向声子晶体柱壳的隔声 表 3 流体介质的声学常数表
特性，所以此处针对径向声子晶体柱壳内外声场与 Table 3 Acoustic constants of the fluid
medium
0
-10 密度/ 声速/ 特性阻抗/
名称 温度/ C
◦
-20 (kg·m −3 ) (m·s −1 ) (Ns·m −3 )
-30 空气 20 1.21 344 415
IL/dB -40 6
-50
-60 甲醇 20 791 1121 0.887 × 10
-70 甘油 20 1261 1923 2.425 × 10 6
-80
-90
-100 3.1 内声场流体介质特性阻抗
0 10 20 30 40 50 60 70
ᮠဋ/kHz 假定径向声子晶体柱壳的本体结构和外声场
(a) ஝ϙፇ౧
流体介质 (理想状态下的流体水) 固定不变，通过改
0
-10 变内部流体介质的特性阻抗来探索隔声量频响曲
-20 线的变化规律。
-30 当内部声场介质的阻抗很小时，隔声量频响曲
IL/dB -40 线峰谷相对较多，随着阻抗的增加，其数量也逐渐减
-50
-60
-70 少。图 8 及图 5(b) 表现出一个共同点，即声波带隙
-80 的位置完全相同，表明声波带隙的位置完全是由径
-90
-100 向声子晶体本体结构所调控。
0 10 20 30 40 50 60 70
ᮠဋ/kHz
3.2 外声场流体介质特性阻抗
(b) దᬍЋ͌ᄾፇ౧
接下来，假定壳体内腔的流体介质为水，径向
图 7 径向声子晶体柱壳的内外声压级之差频响曲线
声子晶体本体结构不变，改变壳体外部声场流体的
Fig. 7 The difference frequency response curve of
特性阻抗参数，使外部声场介质的特性阻抗逐渐增
the inner and outer sound pressure level of cylindri-
cal shell of radial phononic crystals 大，研究隔声量曲线的变化规律。