Page 118 - 201903

400 2019 年 5 月

数值模拟得到的颗粒团运动轨迹与实验数据吻合 2.2.1 原生颗粒半径对颗粒团运动特性的影响
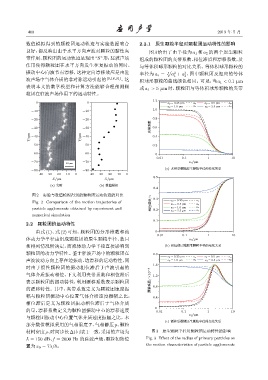
良好，都反映出由于水平方向声波对颗粒的黏性夹 图 3 给出了由半径为 a 1 和 a 2 的两个原生颗粒
带作用，颗粒团的运动轨迹呈现出“S”形；驻波声场 组成的颗粒团的夹带系数、相位滞后和漂移系数，及
作用使得颗粒团在水平方向发生往复振动的同时， 与等体积球形颗粒的对比关系。等体积球形颗粒的
振动中心向波节点漂移，这种定向漂移效应是由驻 √ a + a ，图中颗粒团及相应的等体
3
3
3
半径为 a v =
1 2
波声场中气体介质的非对称运动引起的 [9,18,31] 。这 积球形颗粒的曲线颜色相同。可见，当a 1 < 0.1 µm
表明本文的数学模型和计算方法能够合理预测颗 或 a 1 > 5 µm 时，颗粒团与等体积球形颗粒的夹带
粒团在驻波声场作用下的运动特性。
1.2
0 0 a 2=0.25 µm a v a 2=0.5 µm a v
a 2=1.0 µm a v a 2=2.5 µm a v
1.0
-10 -10
-20 -20 0.8
݃ࣜጇ஝ 0.6
-30 -30
Y/µm -40 Y/µm -40 0.4

-50 -50 0.2
-60 -60 0
0.01 0.1 1 10
-70 -70 a 1 /µm
10 mm
(a) ݃ࣜጇ஝ᬤԔၷᮤዢӧय़ᄊԫӑТጇ
-80 -80
-40 -30 -20 -10 0 -40 -30 -20 -10 0
0.5
X/µm X/µm
(a) ࠄᰎ (b) ஝ϙവલ
0.4
图 2 实验与数值模拟得到的颗粒团运动轨迹的对比
Fig. 2 Comparison of the motion trajectories of ᄱͯ໕Ց/p 0.3 a 2 =0.25 µm a v
a 2 =0.5 µm
a v
particle agglomerate obtained by experiment and 0.2 a 2 =2.5 µm a v
a 2 =1.0 µm
a v
numerical simulation
0.1
2.2 颗粒团的运动特性
由式 (1)、式 (2) 可知，颗粒团的分形维数和流 0
0.01 0.1 1 10
体动力学半径由组成颗粒团的原生颗粒半径、数目 a 1 /µm
和排列情况所决定，而流体动力学半径直接影响到 (b) ᄱͯ໕ՑᬤԔၷᮤዢӧय़ᄊԫӑТጇ
颗粒团的动力学特性。鉴于驻波声场中的颗粒团在 2.0
a 2 =0.25 µm a v a 2 =0.5 µm a v
声波波动方向上存在边振动、边漂移的运动特性，同 a 2 =1.0 µm a v a 2 =2.5 µm a v
1.6
时由于惯性颗粒团的振动相位滞后于声波引起的
气体介质振动相位，下文利用夹带系数和相位滞后 1.2
表示颗粒团的振动特性，利用漂移系数表示颗粒团 ໡ረጇ஝/T10 -3
的漂移特性。其中，夹带系数定义为颗粒团速度振 0.8
幅与颗粒团振动中心位置气体介质速度振幅之比， 0.4
相位滞后定义为颗粒团振动相位滞后于气体介质
0
的量，漂移系数定义为颗粒团振动中心的漂移速度 0.01 0.1 1 10
a 1 /µm
与颗粒团振动中心位置气体介质速度振幅之比。本
(c) ໡ረጇ஝ᬤԔၷᮤዢӧय़ᄊԫӑТጇ
部分数值模拟采用的气相温度 T、气相静压 p、颗粒
材料密度ρ、时间步长∆t同表1一致，采用的声场为 图 3 原生颗粒半径对颗粒团运动特性的影响
L = 150 dB、f = 2000 Hz 的驻波声场，颗粒初始位 Fig. 3 Effect of the radius of primary particles on
置为x 0 = 7λ/8。 the motion characteristics of particle agglomerate