Page 125 - 应用声学2019年第4期

第 38 卷 第 4 期 胡吉英等： 应用长度极化压电陶瓷 33 模态的半主动减振技术研究 585

当考虑压电片厚度对横梁自由端振幅的影响时，将 ԍႃྟ
厚度作为唯一的变量，并将其他参数均设为相同 ഷ್
的。横梁的尺寸设为 630 mm × 30 mm × 1.3 mm， (a) ʷྟԍႃྟ
压电片的长度为 30 mm，将压电片的长度设为远
ԍႃྟ ԍႃྟ
小于横梁尺寸是为了确保尽量减小对横梁振动模
ഷ್
态的影响。提取横梁自由端的振幅，并用压电片
(b) ːྟԍႃྟ
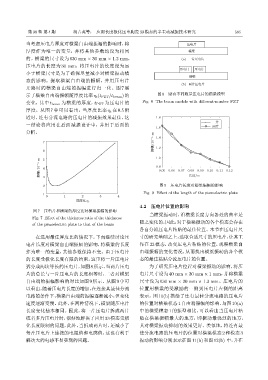
开路时的横梁自由端的振幅进行归一化。图 7 展
示了横梁自由端振幅随厚度比率 η t (t PZT /t beam ) 的 图 8 贴有不同数量压电片的横梁模型
变化，其中 t beam 为横梁的厚度，t PZT 为压电片的 Fig. 8 The beam models with different-number PZT
厚度。从图 7 中可以看出，当厚度比率 η t 在 0.5 附
近时，连有分流电路的压电片的减振效果最佳，这 1.8
ʷྟ
一结论将应用在后面减振设计中，并用于后面的
1.6 ːྟ
分析。
૝ࣨ/10 -4 m 1.4
7
6 1.2
1.0
૝ࣨ/10 -4 m 4 3 0.8 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12
5

᫂ए/m

2 图 9 压电片长度对横梁振幅的影响
Fig. 9 Effect of the length of the piezoelectric plate
1
0 1 2 3 4
Ԓएඋ η t
4.2 压电片位置的影响
图 7 压电片和横梁的厚度比对横梁振幅的影响
当横梁振动时，沿横梁长度方向各处的曲率是
Fig. 7 Effect of the thickness ratio of the thickness
随之变化的，因此，对于横梁振动的各个模态会存在
of the piezoelectric plate to that of the beam
各自分流压电片粘贴的最佳位置。本节在压电片尺
在选用最佳厚度比的情况下，下面继续讨论压 寸的研究基础之上，选取合适尺寸的压电片，让其工
电片长度对横梁自由端振幅的影响，将横梁的长度 作在 33 模态，改变压电片粘贴的位置，观察横梁自
作为唯一的变量，其他参数保持不变。由于压电片 由端振幅的变化情况，从而找出横梁振动的各个模
的长度受极化长度有限的约束，这里将一片压电片 态的最佳粘贴分流压电片的位置。
拆分成两块等长的压电片，如图 8所示，当两片压电 为了研究压电片位置对横梁振动的影响，将压
片的总长与一片压电片的长度相等时，二者对横梁 电片尺寸设为 40 mm × 30 mm × 1 mm，并将横梁
自由端的振幅影响的对比如图 9 所示。从图 9 中可 尺寸设为 630 mm × 30 mm × 1.3 mm。压电片的
以看出，随着压电片长度的增加，在连接其最佳分流 位置用横梁的受激励的一侧到压电片左侧的距离
电路的条件下，横梁自由端的振幅逐渐减小，但变化 表示。图 10(b) 描绘了连有最佳分流电路的压电片
速度逐渐变慢。此外，在两种情况下，横梁随压电片 的位置对横梁模态 1 自由端振幅的影响，与图 10(a)
长度变化基本相同。因此，将一片压电片拆成两片 中的横梁模态 1 的振型相比，可以看出当压电片粘
或者多片压电片时，很好地解决了应用33模态受极 贴在横梁振幅最大的地方，即振动最强烈的地方，

化长度限制的问题，此外，当拆成两片时，还减小了 其对横梁振动抑制的效果更好。类似地，将连有最
每片压电片上连接的电阻值和电感值，这也有利于 佳分流电路的压电片的位置对横梁模态 2 和模态 3
解决大的电感不易实现的问题。 振动的影响分别表示在图11(b)和图12(b) 中，并在