Page 139 - 应用声学2019年第4期

第 38 卷 第 4 期 朱少豪等： 质点振速传感器直线阵超指向性波束形成 599

需要增加到声压阵长度的四倍。因此，由有指向性 那么基于乘积定理的阵列流形向量可定义为
阵元组成的超指向性阵列，能否得到预期的效果，结
ˆ
果尚不明确，有待进一步深入研究。 P (θ, ϕ) = cos θ · [p 1 , p 2 , · · · , p m , · · · , p M ] T
= cos θ · P (θ, ϕ) . (23)
1.0
j 0
0.8 j 1
0.6 j 2 这与质点振速传感器的阵列流形向量相同，波束响
3(j 1/x-j 2)
0.4 应可重写为
0.2
ᄱТጇ஝ -0.2 0 B (θ, ϕ) = B (θ, ϕ) cos θ. (24)
ˆ

-0.4
进一步的，基于乘积定理的指向性因子推导如下
-0.6
-0.8
ˆ
|B (θ 0 , ϕ 0 ) | 2
-1.0
c
0 0.4 0.8 1.2 1.6 2.0 DF = ∫ 2π ∫ π
d⊳λ 1 2
ˆ
|B (θ, ϕ) | sin θdθdϕ
4π 0 0
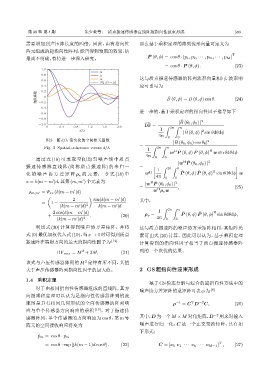
图 3 随 d/λ 值变化的空间相关函数 2
|B (θ 0 , ϕ 0 ) cos θ 0 |
=
Fig. 3 Spatial-coherence versus d/λ 1 ∫ 2π ∫ π
H
H ˆ
ˆ
w P (θ, ϕ) P (θ, ϕ) w sin θdθdϕ
4π 0 0
通过式 (18) 可求取空间均匀噪声场中质点
H ˆ
|w P (θ 0 , ϕ 0 ) | 2
振速传感器直线阵 (简称质点振速阵) 的未归一 = [ ∫ 2π ∫ π ]
1 H
ˆ
ˆ
化 的 噪 声 协 方 差 矩 阵 ρ v 的 元 素， 令 式 (18) 中 w H P (θ, ϕ) P (θ, ϕ) sin θdθdϕ w
4π 0 0
x = k|m − m |d，其第(m, m )个元素为 H ˆ 2
′
′
|w P (θ 0 , ϕ 0 ) |
= H , (25)
ρ m,m = Ψ zz (k|m − m |d) w ρ v w
′
′
( )
′
2 sin(k|m − m |d) 其中，
= 1 −
(k|m − m |d) 2 k|m − m |d
′
′
∫ 2π ∫ π
′
H
2 cos(k|m − m |d) ρ v = 1 P (θ, ϕ) P (θ, ϕ) sin θdθdϕ,
ˆ
ˆ
+ . (20)
(k|m − m |d) 2 4π 0 0
′
利用式 (20) 计算得到噪声协方差矩阵，并将 这与质点振速阵的噪声协方差矩阵相同，其矩阵元
式 (9)最优加权代入式(10)，当x → 0时可得到质点 素可由式 (20) 计算。因此可以认为，基于乘积定理
振速阵在端射方向的最大的指向性因子为 [12] 计算得到的指向性因子相当于质点振速传感器阵
2
DF max = M + 2M. (21) 列的一个次优的结果。
该式与声压传感器阵列的 M 定律有所不同，其值
2
大于声压传感器阵列指向性因子的最大值。 2 GS超指向性波束形成
1.4 乘积定理
基于 GS 模态分解与综合的超指向性方法中的
对于由相同指向性传感器组成的直线阵，其方
噪声协方差矩阵的逆矩阵可表示为 [9]
向图乘积定理可以认为是指向性传感器阵列的波
T
束图是具有相同几何形状的全向传感器的阵列响 ρ −1 = C D −2 C, (26)
应与单个传感器方向响应的乘积 [13] 。对于振速传
感器阵列，单个传感器的方向响应为 cos θ，第 m 号 其中，D 为一个M × M 对角矩阵，D −2 用来对输入
阵元的空间接收响应将变为 噪声进行归一化，C 是一个正交变换矩阵，具有如
下形式：
ˆ p m = cos θ · p m
T
= cos θ · exp [jk(m − 1)d cos θ] . (22) C = [c 0 c 1 · · · c k · · · c M−1 ] , (27)