Page 231 - 应用声学2019年第4期

第 38 卷 第 4 期 高善国等： 正交曲线坐标系在变化地形声场计算中的应用 691

的两组曲线。若计 P 点横坐标为 x 0 = C 2 /C 1 ，则可
设新坐标变量如下：
ງए  ( z )


x ϕ = arctan(C 1 F) = arctan ,
z=f↼x↽ x 0 − x (21)
z √
 √ 2
ᡰሏ  ρ = 2G = z + (x − x 0 ) .
2

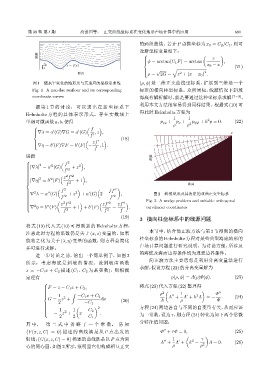
图 1 随水平变化的地形及与其适应的坐标系曲线 (ρ, ϕ) 是二维正交曲线坐标系，扩展到三维是一个
Fig. 1 A non-flat seafloor and its corresponding 标准的横向柱坐标系。众所周知，线源情况下斜坡
coordinate curves 海底有解析解时，就是要通过这种坐标系求解 [7−9] 。
利用本文方法很容易得到同样结果。根据式(10) 可
据第 1 节的讨论， 可以求出在新坐标系下
得此时Helmholtz方程为
Helmholtz 方程的具体表示形式。存在实数域上
1 1
2
单调可微函数a、b，使得 p ρρ + p ρ + p ϕϕ + k p = 0. (22)
ρ ρ 2
 ( f )
∇λ = a (G)∇G = a (G) , z ,
′
′

 P
f ′
(18)
( ′ )
 zf
 ′ ′
∇η = b (F)∇F = b (F) − , 1 .
f
进而 ງए

( f 2 )
 2 ′2 2
|∇λ| = a (G) + z ,

 f ′2



 ( 2 ′2 )
 z f
 2 ′2
|∇η| = b (F) + 1 ,

 2
f ᡰሏ
( 2 ) ( ′′ )
 f ff
2
 ∇ λ = a (G) + z 2 ′ , 图 2 斜坡地形及其决定的双曲正交坐标系
′′

 ′2 + a (G) 2 − ′2
 f f


 ( Fig. 2 A wedge problem and suitable orthogonal
 2 ′2 ) ( ′2
 z f zf zf ′′ )
 2
′′
∇ η = b (F) + 1 + b (F) − . curvilinear coordinates
′

f 2 f 2 f
(19) 3 横向柱坐标系中的线源问题
将式 (19) 代入式 (10) 可得到新的 Helmholtz 方程，
注意此时方程的系数仍是关于 (x, z) 变量的，如果 本节中，结合简正波方法与第 2 节得到的横向
柱坐标系的 Helmholtz方程对某些典型海底地形的
能将之化为关于 (λ, η) 变量的函数，则方程会简化
声场计算问题进行研究说明。为讨论方便，所涉及
并可进行求解。
的海底及海面边界条件均为理想边界条件。
进一步讨论之前，给出一个简单例子，如图 2
简正波方法主要思想是利用分离变量法进行
所示，考虑海底是斜坡的情况。设斜坡由函数
求解，假设方程(22)的分离变量解为
z = −C 1 x + C 2 描述 (C 1 、C 2 为某实数)，则根据
定理有 p(ρ, ϕ) = Λ(ρ)Φ(ϕ). (23)

F = z − C 1 x + C 2 , 将式(23)代入方程(22)整理得

 ( )
 2 ′′
 ∫ ρ 1 Φ
 2
′
′′
 1 2 −C 1 x + C 2 Λ + Λ + k Λ = − . (24)
G = z + dx (20) Λ ρ Φ
2 −C 1

 方程 (24) 两边各自与不同的自变量有关，从而应该
 ( ) 2

 1 1 C 2
 2
 = z + x − . 为一常数，设为 τ，则方程 (24)转化为如下两个常微
2 2 C 1
分特征值问题：
其 中， 第 二 式 中 省 略 了 一 个 常 数。 易 知
{F(x, z, C) = 0} 描述的曲线族是从 P 点出发的 Φ + τΦ = 0, (25)
′′
( )
射线，{G(x, z, C) = 0} 描述的曲线族是以P 点为圆 1 2 τ
′′
′
Λ + Λ + k − Λ = 0. (26)
心的同心圆，如图2 所示，很明显它们构成相互正交 ρ ρ 2