Page 246 - 应用声学2019年第4期

706 2019 年 7 月

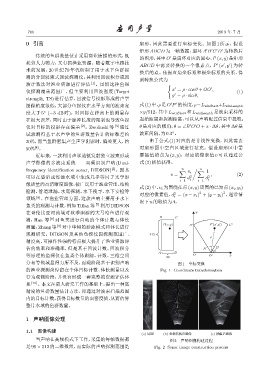
0 引言 扇形，因此需要进行坐标变化。如图 1 所示，假设

矩形 ABCD 为一帧数据，扇环 A B C D 为转换后
′
′
′
′
传统的鱼群数量估计采用商业捕捞的形式，既
的图形，其中 O 是扇环对应的圆心，P (x, y)是矩形
′
耗费人力物力，又有损渔业资源。随着数字电路技
ABCD 中需要转换的一个像素点，P (x , y ) 为转
′
′
′
术的发展，20 世纪 70 年代研制了用于水下鱼群探
换后的点。依据直角坐标系和极坐标系的关系，得
测的分裂波束式回波探测仪，其利用回波积分或回
到转换公式为
波计数法对渔业资源进行评估 [1] 。虽然这种鱼探 {
x = ρ · cos θ + OO ,
′
′
仪探测覆盖范围广，但主要利用回波强度 (Target (1)
′
y = ρ · sin θ,
strength, TS) 进行估算，回波信号投影形成的声学
′
′
图像精度很低，大部分鱼探仪在水平方向的波束宽 式(1)中，ρ是O P 的长度，ρ=L winStart +L winLength
度大于 5 (−3 dB 时)，对目标在距离上的测量存 ×y/512，其中 L winStart 和 L winLength 是波束采样的
◦
在很大误差，同时由于脉冲长度的限制也导致鱼探 起始距离和探测距离，可以从声呐配置信息中提取；
仪对目标的投影存在偏差 [2] 。Zwolinski 等 [3] 通过 θ 是对应的极角，θ = ∠B O O + x · ∆θ，其中 ∆θ 是
′
′
◦
试验测得基于水声学的鱼群数量估计的标准差约 波束间隔，为0.3 。
20%，而当鱼群密集产生声学阴影时，偏差更大，约 由于公式 (1) 对应的是非线性变换，因此需要
50% 。 对扇形图中空白区域进行填充。假设扇形区中需
[4]
近年来，一款利用声学透镜发射独立波束形成 要插值的点为 (x, y)，对应的像素值 v 可以通过公
声学影像的多波束系统 ——双频识别声呐 (Dual- 式 (2)插值获得。
n
[5]
frequency identification sonar, DIDSON) ，因其 ∑ / n 1
∑
v = v i , (2)
可以在昏暗或浑浊水域中生成几乎等同于光学影 d 2 d 2
i=1 i i=1 i
像质量的高清晰度图像，被广泛用于渔业管理、结构
式 (2) 中，v i 为围绕在点 (x, y) 周围的已知点 (x i , y i )
检测、管道泄漏、水底探测、水下搜寻、水下安检等
2
2
对应的像素值，d = (x − x i ) + (y − y i ) ，通常情
2
领域 [6] 。在渔业管理方面，这款声呐主要用于水下 i
况下n的取值为4。
鱼类的观测与计数，例如 Tiffan 等 [7] 利用 DIDSON
在哥伦比亚河流域对秋季洄游的大马哈鱼进行观 y
B C
测，Han 等 [8] 对鱼类进行自动的个体计数与体长
P↼x֒y↽ B ϕ P ϕ↼xϕ֒yϕ↽ C ϕ
测量，Zhang 等 [9] 对中华鲟的游泳模式和体长进行
观测研究。DIDSON 及其他鱼探仪因探测范围广、 
ρ
精度高、可操作性强的特点极大提升了渔业资源评
估的效率和准确率，但是基于回波计数、回波积分 Aϕ Dϕ
A D θ
等原理的鱼探仪在鱼类个体跟踪、计数、三维空间  O O ϕ x
分布等领域显得力所不及，而现阶段基于识别声呐 图 1 坐标变换
的渔业探测尚停留在个体目标计数、体长测量以及 Fig. 1 Coordinate transformation
行为观测阶段，并没有形成一套完整的资源评估体
系 [10] 。本文在前人研究工作的基础上，提出一种高
精度的鱼群数量估计方法，即通过对波束扫描范围
内的目标计数，获得目标数量的面密度值，从而估算
整片水域的鱼群数量。
1 声呐图像处理
1.1 图像构建
(a) Ԕڏ (b) گಖᣁ૱Ցڏϸ (c) ଣϙՑڏϸ
当声呐在高频模式下工作，采集的每帧数据都 图 2 声呐图像构建过程
是 96 × 512 的二维数组，而实际的声呐探测范围是 Fig. 2 Sonar image construction process