Page 13 - 应用声学2019年第5期

第 38 卷 第 5 期 胥利文等： 一维 Marchenko 自聚焦算法的数值解与解析解 765

和第二个序列的幅值相反，它们的叠加将会去除这 接收的波场。如果将上行格林函数和下行格林函数
+
些序列，Θ{R(t) ∗ f 1m }的迭代目的就是要让图 7(b) 求和，可以得到点源激发的全波场。
的幅度接近图 7(a) 中的幅度，从而去除这些伪序
1.0
列的影响，这与理论分析相契合。对于图 7(c) 的结 0.8
䎞䁾ㆂ⺜
果，f (t)中的两个序列的相位差也是2 ∗ t 2 ，作用与 0.6 㤔ㆃㆂ⺜
−
1 0.4
f (t)中的相同，迭代在第六次的时候已经稳定了。 0.2
+
1 ॆʷӑࣨए 0
1.0 -0.2
0.8 -0.4
0.6 -0.6
ॆʷӑࣨए 0.2 0 0 0.4 0.8 ௑ᫎ/s 1.2 1.6 2.0
0.4
-0.8
-0.2
-0.4 (a) ൤໦ʽᛡಫ౤Ѧ஝ˁMarchenkoරᝍፇ౧ࠫඋ
-0.6 1.0
-0.8 0.8
0 0.4 0.8 1.2 1.6 2.0 0.6 䎞䁾ㆂ⺜
௑ᫎ/s 0.4 㤔ㆃㆂ⺜
+ 0.2
(a) Θ{R↼t↽⇀f d ℘ ॆʷӑࣨए 0
0.4 -0.2
-0.15 -0.4
0.3 ֻ၂Ց
-0.20 ኄ̋൓ -0.6
-0.8
0.2
ॆʷӑࣨए 0.1 0 0.45 0.50 0.55 -1.0 0 0.4 0.8 ௑ᫎ/s 1.2 1.6 2.0
ኄО൓
-0.25

-0.1 (b) ൤໦ʾᛡಫ౤Ѧ஝ˁMarchenkoරᝍፇ౧ࠫඋ
-0.2
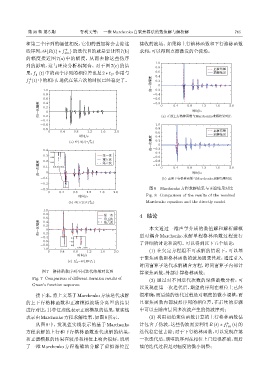
-0.3 图 8 Marchenko 方程求解结果与正演结果对比
0 0.4 0.8 1.2 1.6 2.0
௑ᫎ/s Fig. 8 Comparison of the results of the resolved
+ Marchenko equation and the directly model
(b) Θ{R↼t↽⇀f m ℘
1.0
0.8 ֻ၂Ց 4 结论
0.6 ኄ̋൓
ॆʷӑࣨए 0.2 0 本文通过一维声学介质的数值解和解析解模
0.4
ኄО൓
-0.2
-0.4 -0.4 型对耦合 Marchenko 求解单程格林函数过程进行
-0.6 -0.6 了详细的讨论和说明。可以得到以下五个结论：
-0.8 -0.8

-1.0 0.45 0.50
0 0.4 0.8 1.2 1.6 2.0 (1) 在欠定方程组不可求解的情况下，可以基
௑ᫎ/s
于聚焦函数和格林函数的波场因果性质，通过引入
+ -
(c) f d -Θ{R⇀f  }
时间窗算子迭代求解耦合方程，时间窗算子内部计
图 7 格林函数序列不同迭代结果对比图 算聚焦函数，外部计算格林函数；
Fig. 7 Comparison of different iteration results of
(2) 通过对不同迭代次数的聚焦函数分析，可
Green’s function sequence
以发现在第一次迭代后，期望的序列在相位上已经
接下来，将上文基于 Marchenko 方法迭代求解 很准确，而后续的迭代过程是对幅度的微小调整，而
的上下行格林函数和正演模拟波场分离 [8] 的结果 且聚焦函数内部波形序列的相位差，在后续的步骤
进行对比，其中红虚线表示正演模拟的结果，蓝实线 中可以去除由层间多次波产生的伪波序列；
表示由Marchenko方程求解结果，如图8所示。 (3) 利用初始聚焦函数计算的上行格林函数估
从图 8 中，发现蓝实线表示的基于 Marchenko 计包含了伪波，这些伪波需要利用 R (t) ∗ f + (t) 的
1m
方程求解的上行和下行格林函数迭代求解的结果， 迭代稳定值去除；对于下行格林函数，可以发现在第
和正演模拟的结果在波形和相位上吻合很好，说明 一次迭代后，期望的序列在相位上已经很准确，而后
了一维 Marchenko 方程准确地分解了虚拟源位置 续的迭代过程是对幅度的微小调整；