Page 11 - 应用声学2019年第5期

第 38 卷 第 5 期 胥利文等： 一维 Marchenko 自聚焦算法的数值解与解析解 763

1.0 首先 f + (t) 的初始值为 0，第一步可用 R (t) 和
0.8 0.5 ኄʷ൓ 1m
+
0.6 -0.5 0 ኄ̋൓ f (t) 卷积后，加窗算子 Θ 求取上行格林函数，得到
ኄО൓
1d
0.4
ॆʷӑࣨए -0.2 0 0.2 0.25 0.3 0.35 Θ R(t) ∗ f (t) ： { + }
}
{
+
0.2
1d
−
-0.4 G (t) = Θ R (t) ∗ f 1d (t)
-0.6 + ( 1 )
-0.8 = R A3 f δ t − t 1 − 3t 2 + t 3
1dA
-1.0 2
-0.8 -0.4 0 0.4 0.8 + ( 3 )
௑ᫎ/s + R A4 f 1dA δ t − t 1 − t 2 − t 3
2
-
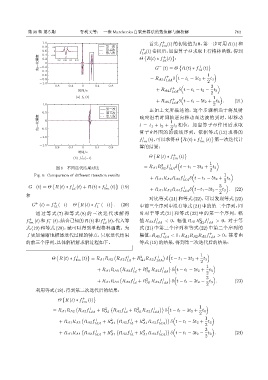
(a) f  ↼t↽ ( 1 )
+ R A5 f + δ t − t 1 − 5t 2 + t 3 . (21)
1.0 1dA 2
ֻ၂Ց 正如上文所描述的，这个步骤相当于将反射
0.5 ኄ̋൓ 响应沿着时间轴逆向移动直达波的到时，即移动
ॆʷӑࣨए 0 t = t 1 + t 2 + 1 t 3 相位，加窗算子 Θ 作用后求取
ኄО൓
2
-0.5
算子 θ 外围的的波场序列。依据等式 (12) 求得的
-1.0 + { + }
f (t)，可以求得 Θ R (t) ∗ f (t) 第一次迭代计
1m 1m
-1.5
-0.8 -0.4 0 0.4 0.8 算的结果：
௑ᫎ/s
{ + }
+ Θ R (t) ∗ f (t)
(b) f m ↼֓t↽ 1m
( 1 )
2
+
f
图 6 不同迭代结果对比 = R A1 R A2 1dA δ t − t 1 − 3t 2 + t 3
2
Fig. 6 Comparison of different iteration results + ( 1 )
+ R A1 R A2 R A3 f
1dA δ t − t 1 − 5t 2 + t 3
2
{ + + } ( )
−
G (t) = Θ R (t) ∗ f (t) + R (t) ∗ f (t) (19) + 3
1d 1m + R A1 R A2 R A4 f δ t−t 1 −3t 2 − t 3 . (22)
1dA 2
和
对比等式 (21) 和等式 (22)，可以发现等式 (22)
}
{
+
−
G (t) = f + (−t) − Θ R (t) ∗ f (−t) . (20) 中前三个序列中没有等式 (21) 中的第二个序列，同
1d 1
通过等式 (7) 和等式 (8) 的三次迭代求解得 时对于等式 (21) 和等式 (22) 中的第一个序列，幅
f + (t)和f (t)，结合已知的R (t)和f + (t)，代入等 值 R A3 f + < 0，幅值 R A1 R 2 f + > 0，对于等
−
1m 1 1d 1dA A2 1dA
式 (19) 和等式 (20)，就可以得到单程格林函数。为 式 (21) 中第三个序列和等式 (22) 中第二个序列的
了更加清晰地描述迭代过程的特点，只取迭代结果 幅值，R A5 f + < 0，R A1 R A2 R A3 f + > 0。接着由
1dA 1dA
的前三个序列，具体解析解求解过程如下。 等式(15)的结果，得到第二次迭代后的结果：
( )
{ + } ( + 2 + ) 1
Θ R (t) ∗ f (t) = R A1 R A2 R A2 f + R R A2 f
1m 1d A1 1dA δ t − t 1 − 3t 2 + t 3
2
( )
( + 2 + ) 1
+ R A1 R A3 R A2 f + R R A2 f δ t − t 1 − 5t 2 + t 3
1d A1 1dA 2
( )
( + 2 + ) 3
+ R A1 R A4 R A2 f + R R A2 f δ t − t 1 − 3t 2 − t 3 . (23)
1d A1 1dA 2
利用等式(18)，得到第三次迭代后的结果：
{ + }
Θ R (t) ∗ f 1m (t)
( )
( + 2 ( + 2 + )) 1
= R A1 R A2 R A2 f + R R A2 f + R R A2 f
1dA A1 1d A1 1dA δ t − t 1 − 3t 2 + t 3
2
( )
( + 2 ( + 2 + )) 1
+ R A1 R A3 R A2 f + R R A2 f + R R A2 f
1dA A1 1d A1 1dA δ t − t 1 − 5t 2 + t 3
2
( )
( + 2 ( + 2 + )) 3
+ R A1 R A4 R A2 f + R R A2 f + R R A2 f δ t − t 1 − 3t 2 − t 3 . (24)
1dA A1 1d A1 1dA
2