Page 8 - 应用声学2019年第5期

760 2019 年 9 月

+
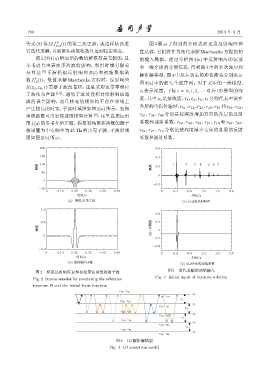
等式 (8) 得到 f 1m (t) 的第二次更新，就这样依次进 图 3 展示了得到的介质表面记录反射响应和
行迭代求解，直到聚焦函数收敛且达到稳定状态。 直达波，它们将作为迭代求解 Marchenko 方程的初
假定图 1(a) 所展示的数值解模型是无损的，且 始输入数据。通过分析图 3(a) 中反射响应的记录
不考虑自由表面多次波的影响，利用时域有限差
和一维介质的分层信息，得到图 4 中的多次波序列
分算法 [9] 正演模拟反射响应 R(t) 和初始聚焦函
解析解模型，图 4 中从左到右的彩色箭头分别表示
+
数 f (t)。数值求解 Marchenko 方程时，反射响应
1d 图 3(a) 中的前七个波序列。对于文中的一维模型，
R(z 0 , z 0 , t) 需要子波反卷积，这里采用宽带零相位
z i 表示深度，下标 i = 0, 1, 2, · · · 对应 1D 模型的深
子波作为声源 [10] ，避免子波反卷积对反射响应造
度，其中 z 0 是接收面，t 1 、t 2 、t 3 、t 4 分别代表声波在
成的误差影响，而且较宽的频带将不会在时域上
各层的单程传输时，r 01 、r 12 、r 23 、r 34 、r 45 和τ 01 、τ 12 、
产生较长的时宽，子波时域图如图 2(a) 所示。初始
聚焦函数可由宏观速度模型计算 [3] ，这里直接运用 τ 23 、τ 34 、τ 45 分别是按深度增加方向的各层的反射
图 1(a)的参考介质正演。模拟初始聚焦函数的源子 系数和透射系数，r 54 、r 43 、r 32 、r 21 、r 10 和 τ 54 、τ 43 、
波设置为中心频率为 25 Hz 的雷克子波，子波时域 τ 32 、τ 21 、τ 10 分别是按深度减小方向的各层的反射
图如图2(b)所示。 系数和透射系数。

200 0.6
150 0.4
ࣨए 100 ࣨए 0.2 1 2 3 4 5 6 7
50
0
0
-0.2
-50
0 0.10 0.20 0.30 0.40 0.50 0 0.4 0.8 1.2 1.6 2.0
௑ᫎ/s ௑ᫎ/s
(a) വલ R ᄊߕฉ (a) ᝮैᄊԦ࠱־ऄ

1.0
0.8
0.5 0.4
ࣨए ॆʷӑࣨए 0

0
-0.4
-0.8
-0.5
0 0.10 0.20 0.30 0.40 0.50 0 0.4 0.8 1.2 1.6 2.0
௑ᫎ/s ௑ᫎ/s
(b) ᘿલູᄊߕฉ (b) ᝮैᄊѺݽᐑཥѦ஝

图 2 模拟反射响应 R 和初始聚焦函数的源子波 图 3 迭代求解的初始输入
Fig. 3 Initial input of iterative solution
Fig. 2 Source wavelet for simulating the reflection
response R and the initial focus function
r 01, τ 
z 0
r 10 , τ 
t 1
r 12 , τ 
z 1
r 21 , τ 
t 2
r 23 , τ 
z 2
r 32, τ 
t 3
r 34 , τ 
z 3
r 43 , τ 
t 4
r 45, τ 
z 4
r 54 , τ 
图 4 1D 解析解模型
Fig. 4 1D analytical model