Page 27 - 应用声学2019年第5期

第 38 卷 第 5 期 张海燕等： 扩散场重建格林函数检测钢轨近表面缺陷 779

1
0
-1
0 10 20 30 40 50 60 70 80 90 100
௑ᫎ/µs
(a) ᄰଌᖍ४ᄊЛᅾ᫼ h i֒j ↼t↽
1
0
-1
400 410 420 430 440 450 460 470 480 490 500
௑ᫎ/µs
(b) ੱஙڤЛᅾ᫼ d i֒j ↼t↽
1
0
-1
-100 -80 -60 -40 -20 0 20 40 60 80 100
௑ᫎ/µs
(c) ಫ౤Ѧ஝־ऄ
1
0
-1
0 10 20 30 40 50 60 70 80 90 100
௑ᫎ/µs
(d) ᧘थᅾ᫼ f i֒j ↼t↽

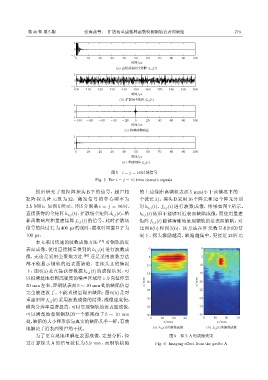
图 5 i = j = 16 时域信号
Fig. 5 For i = j = 16 time domain signals

然后研究了相控阵探头 B 下的信号，超声相 的上边缘距离钢轨表面 5 mm(小于该情况下的一
控阵探头阵元数为 32，激发信号的中心频率为 个波长 λ)。探头 B 采用 16 个阵元和 32 个阵元分别
2.5 MHz，如图 5 所示。图 5 分别是 i = j = 16 时， 对 h i,j (t)、f i,j (t) 进行波数成像，结果如图 7 所示。
直接获得的全矩阵 h i,j (t)、扩散场全矩阵 d i,j (t)、格 h i,j (t) 依旧不能够对近表面缺陷成像，而使用重建
林函数响应和重建矩阵 f i,j (t) 的信号，此时扩散场 矩阵 f i,j (t) 能够清晰地呈现钢轨的近表面缺陷。对
信号的经过T c 为400 µs的延时，截取时间窗口 T 为 比图 6(b) 和图 7(b)，该方法在阵元数量相同的情
100 µs。 况下，探头激励越高，缺陷越集中，更接近 32 阵元
本文采用快速的波数成像方法 [15] 对钢轨的近
表面成像，使用直接测量得到的 h i,j (t) 进行波数成 0 0
像，无论是采用全聚焦方法 [16] 还是采用波数方法 5 5
都不能显示钢轨的近表面缺陷。在探头 A 的情况 10 10
下，图 6(a) 是直接获得数据 h i,j (t) 的成像结果，可
15 15
以很清楚地看到高强度的噪声区域沿 z 方向延伸至 20 20
20 mm 左右，距钢轨表面5 ∼ 10 mm 处的缺陷信息 z/mm z/mm
25 25
完全被湮没了，不能直接呈现出缺陷；图 6(b) 是对
重建矩阵 f i,j (t) 采用波数成像的结果，成像速度快， 30 30
横向分辨率显著提高，可以实现钢轨的近表面成像， 35 35
可以清楚地看到钢轨的一个缺陷位于 5 ∼ 10 mm 40 40
0 10 20 30 0 10 20 30
处，缺陷的大小和形状与真实的缺陷几乎一样，有效 x/mm x/mm
地解决了近表面噪声的干扰。 (a) h i֒j ↼t↽ᄊฉ஝ੇϸ (b) f i֒j ↼t↽ᄊฉ஝ੇϸ
为了更直观地理解近表面成像，定量分析，经 图 6 探头 A 的成像效果
过计算探头 A 的信号波长为 5.9 mm，而钢轨缺陷 Fig. 6 Imaging effect from the probe A