Page 28 - 应用声学2019年第5期

780 2019 年 9 月

0 0 0 0
5 5
5 5
10 10 10 10
15 15 15 15
z/mm 20 z/mm 20 z/mm 20 z/mm 20

25 25 25 25
30 30 30 30
35 35 35 35
40 40
40 40 0 10 20 30 0 10 20 30
0 10 20 30 0 10 20 30
x/mm x/mm x/mm x/mm
(a) 16˔᫼Ћh i֒ j↼t↽ᄊੇϸ (b) 16˔᫼Ћf i֒j↼t↽ᄊੇϸ (c) 32˔᫼Ћh i֒j ↼t↽ᄊੇϸ (d) 32˔᫼Ћf i֒j ↼t↽ᄊੇϸ
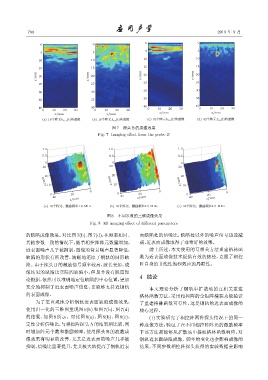
图 7 探头 B 的成像效果
Fig. 7 Imaging effect from the probe B

⊲ ⊲ ⊲
⊲ ⊲ ⊲
  
30 30 30
20 20 20
x/mm 10 x/mm 10 x/mm 10

0 0 0
0 20 0 20 0 20
40 40 z/mm 40
z/mm z/mm
(a) 16˔᫼ЋὊ༏ҵᮠဋ1.0 MHz (b) 16˔᫼ЋὊ༏ҵᮠဋ2.5 MHz (c) 32˔᫼ЋὊ༏ҵᮠဋ2.5 MHz
图 8 不同参数的三维成像效果
Fig. 8 3D imaging effect of different parameters

的缺陷成像效果。对比图7(b)、图7(d)，在频率相同、 面缺陷处的信噪比，缺陷处以外的噪声信号迅速减
其他参数一致的情况下，随着相控阵阵元数量增加， 弱，近表面成像取得了非常好的效果。
近表面噪声几乎被抑制，图像的背景噪声显著降低， 综上所述，本文使用的互相关方法重建格林函

缺陷的形状有所改善，清晰地还原了钢轨的圆形缺 数为近表面成像技术提供有效的捷径，克服了相控
陷。由于探头 B的激励信号频率较高，波长变短，成 阵自身的非线性饱和效应的局限性。
像结果的缺陷比实际的缺陷小，但是并没有脱离理
4 结论
论根据，依然可以准确地定位缺陷的中心位置，更加
充分地抑制了近表面噪声信息，更能够支持近钢轨 本文理论分析了钢轨中扩散场的互相关重建
的表面成像。 格林函数方法，采用相控阵的全矩阵捕获功能验证
为了更直观地分析钢轨近表面缺陷成像效果， 了重建格林函数可行性，这是钢轨的近表面成像的
使用归一化的三维图重现图 6(b) 和图 7(b)、图 7(d) 核心过程。
的结果，如图 8 所示。对比图 8(a)、图 8(b)、图 8(c)， (1) 实验研究了相控阵两种探头情况下的同一
定性分析信噪比，与相控阵探头A的结果相比较，同 种成像方法，验证了在不同相控阵阵元的激励频率
时增加阵元个数和激励频率，使用探头 B 的波数成 下该方法都能够从扩散场中提取格林函数响应，对
像效果有明显的改善，尤其是近表面的噪声几乎被 钢轨近表面缺陷成像。频率的变化也会影响成像的
抑制，信噪比显著提升，尤其极大地提高了钢轨近表 结果，不同参数相控阵探头获得的实验数据会影响