Page 62 - 《应用声学》2019年第6期

964 2019 年 11 月

x − vt 0.95
. (14)
᜺ࠣགᮠဋˁູᮠဋᄊඋϙ w⊳w  0.70
=√ M/⊲
2
(x − vt) + y 2 0.90 M/⊲
所以可以推导出： 0.85 M/⊲
M/⊲
0.80
R 1 = R (1 − M cos θ) . (15) 0.75
O↼x֒y֒z↽ 0.65
0.60
R 0.55
r 0.50
2 4 6 8 10
ᤂүܦູሏन᜺ࠣགᄊ௑ᫎ/s
θ S
x e/Vt e x s/Vt X 图 3 匀亚音速直线运动声源的频移特征
Fig. 3 Frequency shift characteristics of uniform
图 2 匀亚音速运动点源模型
subsonic linear motion sound source
Fig. 2 Uniform subsonic motion point source
model 1.3 声特征提取实现流程
将 STFT-LLE 流形学习方法应用于特征提取，
1.2.2 运动声源特性
弥补传统特征提取方法在处理数据复杂、提取特征
(1)运动声源声辐射特性 维数高、不准确等缺陷 [24] 。STFT-LLE流形学习方

假设运动点源为强度由q 规定的脉动球 [19−20] ， 法的声特征提取流程如图4所示。
其源分布密度可以表示为 q(r, t) = Q S (t)δ(x −
ܦηՂ
vt)δ(y)δ(z)，声压场波动方程 [21] 可表示为
2
1 ∂ p ஝૶ᮕܫေ
2
∇ p − ᧔ၹhammingቔ
2 2
2
c ∂ t STFT ቔࠕԩ˞256
∂
= [Q s (t)δ(x − vt)δ(y)δ(z)]. (16)
∂t ௑ᮠྲढ़ᅾ᫼
当声源低速运动 (M < 0.2) 时，声辐射公式可简化 ԩతᤃ᥶གk/҂
LLE
ࢦК፥஝ d/
为 [21] Ͱ፥ืॎྲढ़
q [t − (R/c)]
′
p (t) = p 1 (t) = 2 , (17) STST-LLEืॎߦ˸வข
4πR (1 − M cos θ)
ᓤ៨ڏ
式 (17) 中，p (t) 为观测点接收信号，q (t) 为声源原
′
始信号。 ืॎྲढ़Ի᜽ӑ
因为 R 是时间的函数，当单频声源以亚音速做 图 4 STFT-LLE 流形学习方法声特征提取流程图
匀速直线运动时，观测点接收到的声信号频率以及 Fig. 4 Flow chart of STFT-LLE manifold learning
幅度均随时间发生变化。这种特征频率的变化在多 method
普勒效应以及指向性特征中均有所体现。 STFT-LLE 流形学习方法的声特征提取具体
(2)多普勒效应 流程如下：
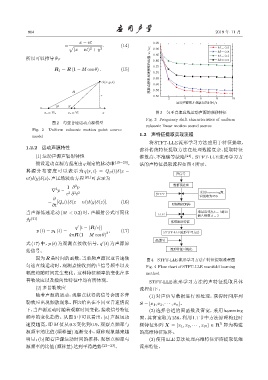
随着声源的运动，观察点获得的信号会因多普 (1) 对声信号数据进行预处理，获得时间序列
勒效应出现频散现象。图 3 给出在不同亚音速情况 S = [x 1 , x 2 , · · · , x n ]。
下，当声源运动时随着观察时间变化，接收信号特征 (2) 选择合适的窗函数及窗宽，采用 hamming
频率的变化趋势。从图 3 中可以看出：(a) 声源运动 窗，其窗宽取为 256，利用 1.1 节中方法原理构建时
D
速度越高，即 M 值从 0.3 变化到 0.9，观察点频率与 频特征矩阵 X = [x 1 , x 2 , · · · , x N ] ∈ R 即为构建
源频率的比值 (频移量) 逐渐变小，频移现象越来越 的高维特征矩阵。
明显；(b) 随着声源运动时间的推移，观察点频率与 (3) 使用 LLE 算法处理高维特征矩阵提取低维
源频率的比值(频移量)达到平稳趋势 [22−23] 。 流形特征。