Page 9 - 《应用声学》2019年第6期

第 38 卷 第 6 期 张国昌等： 使用同心多环阵提升声源定位鲁棒性 911

UCA低阶CH下存在模值无穷大的补偿系数 (图中 畸变，另外，正则化还引起了低频波束的展宽。而
展示的是模值的倒数)，UCCA通过组合两个无公共 UCCA 则不存在上述问题。由于 CH分解阶数的限
贝塞尔函数零点的 UCA 完全解决了这一问题。另 制，在高频区域，DSB方法具有最窄的主瓣。
外值得注意的是，与没有进行正则化处理的两UCA
相比，UCCA 在任一频点下都具有更小的补偿系数
表 1 阵列参数
模值，也就是说，UCCA 在任一频率下都具有更加 Table 1 Configurations of microphone arrays
稳健的性能。图 3 对比了正则化后 UCA 和 UCCA
的波束响应，其中，CH 分解阶数为 3 阶，单环阵半 阵型 各环半径/mm 各环阵元数目
径选择为 60 mm。正则化虽然有效地提升了单环 UCA 40 16
阵CHB的稳健性，但并不能有效地消除贝塞尔函数 UCA 1 60 16
零点导致的波束图失真。正则化 UCA 的波束响应
UCCA [60,40] [9,7]
在2180 Hz、3440 Hz、4630 Hz 等频点处存在明显的

40 mm 60 mm-Reg 40 mm 60 mm-Reg 40 mm 60 mm-Reg
60 mm [40,60] mm 60 mm [40,60] mm 60 mm [40,60] mm
1.5 1.0
0.8
0.8 0.6
||H l (ω,90O) -1 || ||H l (ω,90O) -1 || 0.6 ||H l (ω,90O) -1 || 0.4
1.0

0.4
0.5
0.2
0.2
0 0 0
0 2000 4000 6000 0 2000 4000 6000 0 2000 4000 6000
ᮠဋ/Hz ᮠဋ/Hz ᮠဋ/Hz
(a) ᫽஝=0 (b) ᫽஝=1 (c) ᫽஝=2
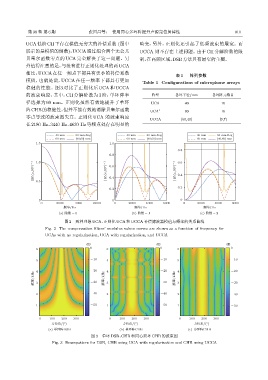
图 2 两种理想 UCA、正则化 UCA 和 UCCA 补偿滤波器模值与频率的关系曲线
Fig. 2 The compensation filters’ modulus values curves are shown as a function of frequency for
UCAs with no regularization, UCA with regularization, and UCCA

dB dB dB
6 0 6 0 6 0

5 -10 5 -10 5 -10

4 -20 4 -20 4 -20
ᮠဋ/kHz 3 -30 ᮠဋ/kHz 3 -30 ᮠဋ/kHz 3 -30

2 -40 2 -40 2 -40

1 -50 1 -50 1 -50

0 100 200 300 0 100 200 300 0 100 200 300
வͯᝈ/(°) வͯᝈ/(°) வͯᝈ/(°)
(a) ӭဗ᫼DSB (b) ӭဗ᫼CHB (c) ܳဗ᫼CHB
图 3 单环 DSB、CHB 和同心双环 CHB 的波束图
Fig. 3 Beampattern for DSB, CHB using UCA with regularization and CHB using UCCA