Page 11 - 《应用声学》2020年第3期

第 39 卷 第 3 期 王舰航等： 超声对近壁微气泡溃灭过程的影响 331

所示，计算域为 500 µm × 250 µm 的矩形区域。边 同时将计算结果与 Rayleigh-Plesset (R-P) 方程的
界 AB 为壁面，壁面是无滑移静止刚性壁面边界条 近似解析解进行对比。不同网格气泡体积变化如
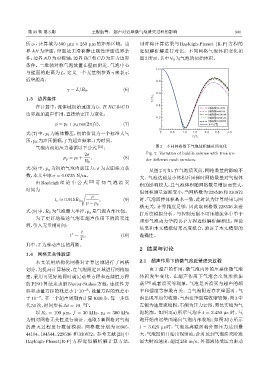
件，边界 AD 为对称轴，边界 BC 和CD 为压力边界 图 2所示，其中V 0 为气泡的初始体积。
条件。二维轴对称气泡放置在壁面附近，气泡中心
⊲
与壁面的距离为 L，定义一个无量纲参数 γ 来表示
近壁距离： ⊲

γ = L/R 0 . (6)
V⊳V 0 ⊲
1.3 边界条件
⊲
在计算中，流体域初始速度为 0。在 BC 和 CD Ꭺಫ஝=16905
边界施加超声作用，直接给定压力变化： Ꭺಫ஝=44104
Ꭺಫ஝=104544
⊲ Ꭺಫ஝=228536
Ꭺಫ஝=330872
p = p l + p d cos(2πft), (7) R-Pவሮ

式 (7) 中，p l 为液体静压，初始值设为一个标准大气  ⊲ ⊲ ⊲ ⊲ ⊲ ⊲
t⊳t c
压，p d 为声压振幅，f 为超声频率，t为时间。
气泡内初始压力遵循以下公式 [21] ： 图 2 不同网格数下气泡体积随时间变化
2σ Fig. 2 Variation of bubble volume with time un-
p g = p l + , (8) der different mesh numbers
R 0
式 (8) 中，p g 为初始气泡内部压力，σ 为表面张力系
从图2可知，在气泡溃灭前，网格数量的影响不
数，本文中取σ = 0.0735 N/m。
大。气泡达到最小体积后回弹时网格数量对气泡体
由 Rayleigh 理 论 中 公 式 [22] 可 知 气 泡 溃 灭
积的影响较大，且气泡体积随网格数量增加而变大，
时间为
√ 但体积增量逐渐变小，当网格数为228536和330872
ρ
t c ≈ 0.915R 0 , (9) 时，气泡回弹体积基本一致，此时认为计算结果与网
p − p g
格无关，计算精度足够，因此取网格数 228536 来进
式(9)中，R 0 为气泡最大半径，p g 是气泡内部压强。
行后续模拟分析。与控制无限不可压缩流体中单个
为了更好地描述气泡在超声作用下的溃灭过
球形气泡动力学的 R-P 方程近似解析解相比，理论
程，引入无量纲时间：
结果和本文模拟结果高度拟合，验证了本文模型的
t
t = , (10) 准确性。
∗
T
其中，T 为驱动声压的周期。
2 结果与讨论
1.4 网格无关性验证
本文采用结构化网格对计算区域进行了网格 2.1 超声作用下的微气泡近壁溃灭过程
划分，为提高计算精度，在气泡附近区域进行网格加 由于超声的作用，微气泡内外的压差使微气泡
密，采用可更好地同时满足动量方程和连续性方程 体积发生变化，在超声作用下气泡会出现形状振
的 PISO 算法来求解 Navier-Stokes 方程，连续性方 荡 [24] 或者溃灭等现象，气泡是否溃灭与超声的频
程和动量方程的残差小于 10 −6 ，能量方程的残差小 率和强度等参数有关。当气泡附近存在壁面时，气
于10 −7 。在一个超声周期内计算1000步，每一步迭 泡出现不均匀收缩，气泡近壁面端收缩较慢，图3 中
代50次，时间步长∆t = 10 −3 T。 左侧为速度流线图，右侧为压力云图，黑色实线为气
以 R 0 = 100 µm、f = 30 kHz、p d = 300 kPa 泡轮廓。如图 3(a) 所示气泡在 t = 3.450 µs 时，气
为例对网格无关性进行验证。选取 5 套网格对气泡 泡开始由远壁面端向气泡内部收缩；如图 3(b) 所示
的溃灭过程进行数值模拟，网格数分别为 16905、 t = 3.620 µs 时，气泡远离壁面端外部压力达到最
44104、104544、228536 和 330872。参考文献 [23] 中 大，气泡凹陷开始出现射流，此时达到气泡溃灭阶段
Rayleigh-Plesset(R-P) 方程近似解析解计算方法， 最大射流速度，超过250 m/s。外部液体受压力驱动