Page 129 - 《应用声学》2020年第4期

第 39 卷 第 4 期 肖梦迪等： 一种能量比调控的有源噪声控制算法 615

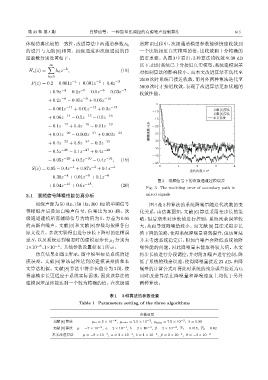
道辨识过程中，次级通道模型参数能够快速收敛到
体现仿真比较的一致性，改进算法中两通道参数h k
的设置与文献 [8] 相同。初级通道和次级通道的传 一个比较接近真实模型的值，比收敛到十分精确的
递函数分别设置如下： 值更重要。从图 3 中看出，3 种算法均收敛至 30 dB

∞ 以下，此时系统已十分接近真实模型，系统建模误差
∑
H s (z) = h k z −k , (18)
对控制算法的影响较小。而本文改进算法在迭代至
k=0
2500 次时系统已接近收敛，而另外两种算法迭代至
P(z) = 0.2 − 0.001z −1 + 0.001z −2 + 0.4z −3
5000 次时才接近收敛，表现了改进算法更加优越的
+ 0.9z −4 − 0.1z −5 − 0.5z −6 − 0.03z −7
收敛性能。
+ 0.2z −8 − 0.05z −9 + 0.05z −10
-5
− 0.001z −11 + 0.01z −12 + 0.3z −13 ஡࿹[6]ካข
-10
஡࿹[8]ካข
+ 0.06z −14 − 0.5z −15 − 0.5z −16 -15 వ஡ካข
− 0.1z −17 + 0.4z −18 − 0.01z −19 -20

+ 0.01z −20 − 0.003z −21 + 0.003z −22 थവឨࣀ/dB -25
+ 0.4z −23 + 0.8z −24 − 0.2z −25 -30
-35
−26
−27
−28
− 0.5z − 0.1z + 0.4z
-40
− 0.05z −29 + 0.2z −30 − 0.4z −31 , (19)
-45
S(z) = 0.05 − 0.4z −1 + 0.87z −2 + 0.1z −3 0 1 2 3 4
ᤖ̽൓஝/10 4
− 0.38z −4 + 0.01z −5 + 0.1z −6
图 3 混频信号下的次级通道建模误差
+ 0.04z −13 + 0.6z −15 . (20)
Fig. 3 The modeling error of secondary path in
3.1 混频信号降噪性能仿真分析 mixed signals
初级声源为50 Hz、150 Hz、300 Hz的单频信号 图 4 是 3 种算法的系统降噪量随迭代次数的变
等幅组合后叠加白噪声信号，信噪比为 30 dB。次 化关系，由仿真图知，文献 [6] 算法采用变步长的策
级通道建模所需辅助信号为均值为 0、方差为 0.05 略，但后期未对步长值进行控制，系统残余误差较
的高斯白噪声。文献 [6] 和文献 [8] 参数均按照各自 大，从而导致降噪量较小。而文献 [8] 算法采用步长
原文设置。多次实验得出进行步长下降时的建模误 值下降的策略，使得系统降噪量得到提升，但该算法
差S，以及系统达到稳态时的建模定步长 µ 1 分别为 并未考虑系统稳定后，附加白噪声会降低系统的降
1×10 −6 、1×10 −3 。其他参数设置如表1所示。 噪性能的问题，因此降噪量未能取得较大值。本文
仿真结果如图 3 所示，图中纵坐标是系统的建 将步长值进行分段调控，并对附加噪声进行控制，降
模误差。文献 [6] 算法最终达到的建模误差值和本 低了系统的残余误差，使得降噪量接近23 dB，由降
文算法相似。文献 [8] 算法中将步长值分为 3 段，使 噪量的计算公式可得此时系统的残余误差接近为0，
得建模步长更适应于系统实际需求，因此该算法的 同时改进算法在降噪量和降噪速度上均优于另外
建模误差最终能达到一个较为精确的值。在次级通 两种算法。

表 1 3 种算法的参数设置
Table 1 Parameters setting of the three algorithms

参数设置
文献 [6] 算法 µ w = 5 × 10 −4 , µ max = 2.5 × 10 −2 , µ min = 7.5 × 10 −3 , λ = 0.99
文献 [8] 算法 µ = −7 × 10 −3 , a = 2 × 10 −1 , b = 2 × 10 −3 , β = 2 × 10 −2 , T 1 = 0.015, T 2 = 0.02
本文改进算法 µ = −8 × 10 −3 , a = 2 × 10 −1 , b = 1 × 10 −3 , β = 2 × 10 −1 , ∂ = −3 × 10 −2