Page 130 - 《应用声学》2020年第4期

616 2020 年 7 月

25 图6 为系统迭代至 30000次时，3 种算法的系统

20 降噪量变化。相较于其他两种算法，本文算法依旧
保持较快的降噪速度和较高的降噪量。由以上仿真
15
ᬌ٪᧚/dB 10 ஡࿹[6]ካข 结果得，本文在降噪量、降噪速度和系统收敛性能方
面都大有改进。与文献 [6] 算法相比，计算量有所增
5 ஡࿹[8]ካข 加，因涉及下降阈值较少，计算量小于文献[8]算法。
వ஡ካข
0
25
-5
0 1 2 3 4
20
ᤖ̽൓஝/10 4
图 4 混频信号下 3 种算法降噪量对比 15
Fig. 4 Comparison of noise reduction of the three ᬌ٪᧚/dB
algorithms in mixed signals 10 ஡࿹[6]ካข
஡࿹[8]ካข
3.2 次级通道变化时算法降噪性能仿真分析 5 వ஡ካข
在实际情况中，次级通道并不是一成不变的，
0
而是随时间不断变化。这就需要控制算法可以快速 1 2 3 4 5
ᤖ̽൓஝/10 4
跟踪这种变化。为体现系统的时变能力，假设系统
迭代至一定次数时次级通道发生突变，其他仿真条 图 6 次级通道突变时的降噪量
件和3.1节相同。次级通道的传递函数为 [8] Fig. 6 The noise reduction when the secondary
path changed abruptly
−1
−2
−3
S(z) = 0.03 − 0.1z + 0.8z + 0.1z
− 0.1z −4 + 0.2z −12 + 0.04z −13 3.3 宽带低频噪声信号降噪性能仿真分析
− 0.01z −14 + 0.6z −15 . (21) 由均值为 0、方差为 1 的高斯白噪声通过通带
为 100 ∼ 400 Hz 带通滤波器产生宽带信号 [14] ，将
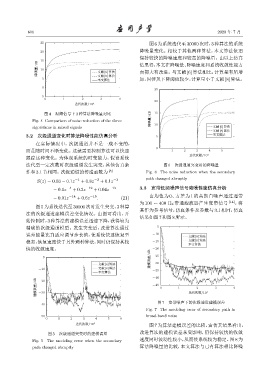
图5 为系统迭代至 30000次时发生突变，3 种算
其作为参考信号，仿真条件及参数与 3.1 相同，仿真
法的次级通道建模误差变化情况。由图可看出，开
结果如图7和图8所示。
始控制时，3 种算法的建模误差迅速下降，获得较为
精确的次级通道模型。发生突变后，改进算法通过 -5
误差能量比自适应调节步长值，使系统快速恢复至 -10 ஡࿹[6]ካข
稳态，恢复速度快于另外两种算法，同时仍保持其较 -15 ஡࿹[8]ካข
వ஡ካข
快的收敛速度。 -20

0 थവឨࣀ/dB -25
஡࿹[6]ካข -30
-10 ஡࿹[8]ካข -35
వ஡ካข
-40
थവឨࣀ/dB -30 -45 0 1 ᤖ̽൓஝/10 4 3 4
-20
2

图 7 宽带噪声下的次级通道建模误差
-40
Fig. 7 The modeling error of secondary path in
-50 broad-band noise
0 1 2 3 4 5 6
ᤖ̽൓஝/10 4 图 7 为算法建模误差的比较，由仿真结果看出，

图 5 次级通道突变时的建模误差 改进算法的建模误差未受影响，仍保持较快的收敛
Fig. 5 The modeling error when the secondary 速度同时波动性较小，从而使系统较为稳定。图8为
path changed abruptly 算法降噪量的比较，本文算法与已有算法相比降噪