Page 34 - 《应用声学》2020年第4期

520 2020 年 7 月

适用于浅海 Pekeris 波导的 warping 函数有如 第m号模的能量可以表示为
下形式： ω=ω 0 +∆ω
∑
√ m 2
( ) 2 E STFT = |F STFT (t m , ω)| , (11)
2
w (t) = t + r/c 0 , (6)
ω=ω 0 −∆ω
其中，r 是传播距离，c 0 是水中声速。经过 warping 其中，ω 0 为信号的中心频率，∆ω 为信号的带宽。
变换后，在新的时轴上，不同频率的第 m 号简正波
m
变成了具有相同角频率 ω 的单频信号。在理想波 3 STFT和warping变换简正波分离性能
w
导情况下， 和海底声衰减反演的比较
ω m = (2m − 1) πc 0 . (7)
w
H 3.1 仿真计算
在新的 warping 频域上，第 m 号简正波的能量
为了更直观地比较 STFT 和 warping变换的简
可以表示为
正波分离性能，下面用仿真计算的例子来进一步讨
v
u m m
u ω +∆ω w
w
∑ 2 论。仿真计算用的环境模型为 Pekeris波导，声源和
m
u
E warp = t |F w (ω)| , (8)
m
ω −∆ω m 接收器均位于海底，参数如图1所示。
w w
m
其中，F w (ω) 是 warping 变换后信号的频谱，ω 是
w
c /1480 m/s
H=30 m
第 m 号模对应的 warping 频率，∆ω 是第 m 号模 Z s /Z r /H ρ  =1.0 g/cm 3
m
w
的半功率点对应的频谱宽度。 a =0 dB/λ
STFT 是传统的分析时变信号频谱特征的信 c b/1580 m/s
ρ b =1.8 g/cm 3
号处理方法，它弥补了常规快速傅里叶变换 (Fast a b=0.3 dB/λ
Fourier transform, FFT)只具有频域分辨率而不具
图 1 Pekeris 环境模型示意图
有时域分辨率，即不适用于分析非平稳信号的不足。
Fig. 1 The environmental parameters in the
它既反映了信号的频率内容，也反映了频率内容随
Pekeris waveguide
时间变化的规律。在浅海波导中，接收声场信号可
以表示为M 号不同时间到达的信号的线性叠加： STFT通过控制时间窗函数的宽度来实现简正
M 波的分离，因此简正波的分离性能受窗函数的影
∑
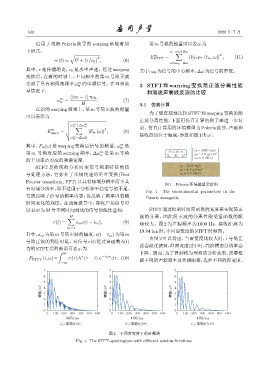
r(t) = a m s(t − t m ), (9) 响较大。图 2 为声源频率为 1000 Hz、接收距离为
m=1
19.84 km时，不同窗宽度的STFT时频图。
其中，a m 为第 m号简正波的幅度，s(t − t m ) 为第 m
由图 2 可以看出，当窗宽度比较大时，1 号简正
号简正波的到达时延。对信号 r(t) 经过窗函数 h(t)
波会被过滤掉，但窗宽度过小时，高阶模态分辨率会
为的STFT后的频谱可表示为
∫ 下降。因而，为了得到较为理想的分析效果，需要根
∞
∗
F STFT (t, ω)= r (τ) h (τ − t) e −iωτ dτ. (10)
据不同的声源频率及传播距离，选择不同的窗宽度。
−∞
7 7 7
6 6 6
5 5 5
ࣨϙ/nV 4 3 ࣨϙ/nV 4 3 ࣨϙ/nV 4 3
2 2 2
1 1 1
0 0 0
0 100 200 300 400 500 600 0 100 200 300 400 500 600 0 100 200 300 400 500 600
௑ᫎ/ms ௑ᫎ/ms ௑ᫎ/ms
(a) ቔࠕए˞51 (b) ቔࠕए˞81 (c) ቔࠕए˞101
图 2 不同窗宽度下的时频谱
Fig. 2 The STFT-spectrogram with different window functions