Page 109 - 《应用声学》2020年第6期

第 39 卷 第 6 期 郭文成等： 平行声屏障的陷波模态及其插入损失优化 903

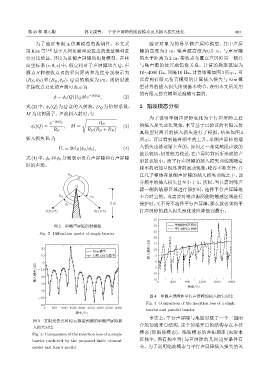
为了验证有限元仿真模型的准确性，本文采 验证对象为简易单侧声屏障模型，其中声屏
用Kim 等 [14] 基于几何衍射理论提出的数值模型进 障的高度为 2 m，噪声源高度为 0.5 m，与声屏障
行对比验证。图 2 为单侧声屏障的衍射模型。在柱 的水平距离为 2 m；接收点布置在声屏障另一侧并
面坐标系 (r, θ, z) 中，假定相对于声屏障顶点 Q，声 与噪声源的位置成镜像关系。计算的频率范围为
源点 S 和接收点 R 的径向距离和角度分别表示为 10∼4000 Hz，间隔 10 Hz，计算结果如图 3 所示。可
(R S , θ S ) 和 (R R , θ R )，Q 点的角度为 νπ。则衍射波 以看到有限元仿真模型的计算插入损失与 Kim 模
在接收点R 处的声场可表示为 型计算的插入损失结果基本吻合，表明本文所采用
的有限元仿真模型是准确可靠的。
ϕ = ϕ i (Q)D Q Me −ikR R , (2)

式 (2) 中，ϕ i (Q) 为 Q 点的入射波，D Q 为衍射系数， 2 陷波模态分析
M 为比例因子。声波斜入射时，有
为了说明单侧声屏障变化为平行声屏障之后
√
e −ikR S R S
ϕ i (Q) = , M = . (3) 的插入损失恶化现象，本节基于已验证的有限元仿
R S R R (R S + R R )
真模型对两者的插入损失进行了模拟，结果如图 4
插入损失IL为 所示。可以看到随着频率的上升，单侧声屏障的插

IL = 20 lg |ϕ 0 /ϕ b | , (4) 入损失也是逐渐上升的。原因之一是高频段声波的
波长较短，衍射能力较差，在声屏障背后所形成的声
式 (4) 中，ϕ 0 和 ϕ b 分别表示没有声屏障和有声屏障
影区也较小。而平行声屏障的插入损失曲线则随着
时的声场。
频率的增加呈现显著的波动现象，峰谷不断交替，并
且几乎整体在单侧声屏障的插入损失曲线之下，部
θ R
νp
分频率的插入损失甚至小于0。所以，当只需对噪声
Q
源一侧的敏感区域进行保护时，选择平行声屏障是
不合时宜的。当需要对噪声源两侧的敏感区域进行
R S
R R
2 m 保护时，又不得不选择平行声屏障，那么就必须将平
θ S
S↼֒⊲↽ R↼֒⊲↽ 行声屏障的插入损失恶化效应降低到最小。
35
图 2 单侧声屏障衍射模型 30 ӭΟѸভܦࡖᬪ
ࣱᛡѸভܦࡖᬪ
25
Fig. 2 Diffraction model of single barrier
20
15
20 ଣК૯ܿ/dB 10
Kimവی
10 దᬍЋ͌ᄾവی 5
0
0 -5
ଣК૯ܿ/dB -10 -10
-20
-30 -15 0 400 800 1200 1600 2000
ᮠဋ/Hz
-40
图 4 单侧声屏障和平行声屏障的插入损失对比
-50
Fig. 4 Comparison of the insertion loss of a single
-60
0 500 1000 1500 2000 2500 3000 3500 4000
barrier and parallel barrier
ᮠဋ/Hz
事实上，平行声屏障与地面形成了一个三面闭
图 3 有限元仿真和 Kim 模型预测的单侧声屏障插
合的顶端开口结构，这个顶端开口的结构存在本征
入损失对比
模态 (即陷波模态)。陷波模态的共振频率 (也称本
Fig. 3 Comparison of the insertion loss of a single
barrier predicted by the proposed finite element 征频率、固有频率等) 与声屏障的几何边界条件有
model and Kim’s model 关。为了说明陷波模态与平行声屏障插入损失的关