Page 111 - 《应用声学》2020年第6期

第 39 卷 第 6 期 郭文成等： 平行声屏障的陷波模态及其插入损失优化 905

对应的设计频率为 520 Hz(即平行声屏障的第 4 阶 提升某一个单频处的插入损失，这在某些具有特殊
陷波模态)，单个空腔的宽度为 0.025 m。吸声型声 声学需求的场所可能会得到较好的应用。而如果想
屏障采用的是绿色环保的无纤维吸声体 ——微穿 改善声屏障在某个倍频程范围内的等效插入损失，
孔板吸声体，吸声体板厚为 0.4 mm，穿孔直径为 那么提高该频段的吸声系数是更好的选择。
0.3 mm，穿孔率为 1%；其吸声系数采用马大猷院
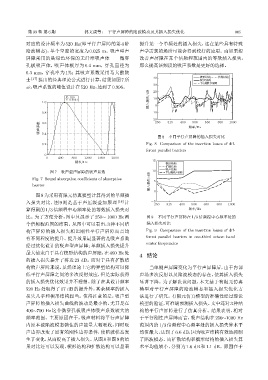
士 [17] 提出的经典理论公式进行计算，结果如图7所 40 ഀॎፇ౞ ੱஙፇ౞
ծܦፇ౞
ࣱᛡѸভܦࡖᬪ
示，吸声系数的峰值设计在520 Hz，达到了0.996。 30
20
X: 520 10
Y: 0.9961 ଣК૯ܿ/dB
1.0 0
0.8 -10
-20 315 400 500 630 800 1000
250
0.6
ծܦጇ஝ ᮠဋ/Hz
0.4
图 8 不同平行声屏障的插入损失对比
0.2 Fig. 8 Comparison of the insertion losses of dif-
ferent parallel barriers
0
0 400 800 1200 1600 2000
15
ᮠဋ/Hz
ഀॎፇ౞
ੱஙፇ౞
ծܦፇ౞
图 7 吸声型声屏障的吸声系数 10 ࣱᛡѸভܦࡖᬪ
ଣК૯ܿ/dB 5
Fig. 7 Sound absorption coefficients of absorptive
barrier
图8 为采用有限元仿真模型计算得到的单频插 0
入损失对比，图 9 则是基于声压级叠加原理 [18] 计 -5 315 400 500 630 800 1000
250
算得到的 1/3倍频程中心频率处的等效插入损失对 ᮠဋ/Hz
比。为了方便分析，图中只展示了 250∼ 1000 Hz 两 图 9 不同平行声屏障在 1/3 倍频程中心频率处的
个倍频程范围的结果。从图中可以看出，3种不同结 插入损失对比
构声屏障的插入损失相比刚性平行声屏障而言均 Fig. 9 Comparison of the insertion losses of dif-
有不同程度的提升。提升效果最显著的是吸声系数 ferent parallel barriers in one-third octave band
center frequencies
经过优化设计的吸声型声屏障；单频插入损失提升
最大值来自于具有楔形结构的声屏障，在460 Hz 处
4 结论
的插入损失提升了将近 23 dB。而对于具有扩散结
构的声屏障来说，虽然理论上它的异型结构可以降 当单侧声屏障变化为平行声屏障后，由于内部
低平行声屏障之间的多次反射效应，但是实际获得 声场多次反射以及陷波模态的存在，使其插入损失
的插入损失优化效果并不理想。除了在其设计频率 显著下降。为了解决该问题，本文基于有限元仿真
520 Hz 处取得了 17 dB 的提升外，其余频率的插入 模型对平行声屏障的陷波模态和插入损失优化方
损失几乎和楔形结构相当。值得注意的是，吸声型 法进行了研究。有限元仿真模型的准确性经过理论
声屏障的插入损失曲线的波动是最小的，尤其是在 模型的验证，可准确预测插入损失。文中还对3种结
400∼700 Hz 这个微穿孔板吸声体吸声系数较大的 构的平行声屏障进行了仿真分析。结果表明，相对
频率范围。主要原因在于，吸声材料将平行声屏障 于平行刚性声屏障而言，吸声结构在 250∼1000 Hz
内原本被陷波模态锁住的声能量大幅吸收，同时吸 范围内的 1/3倍频程中心频率处的插入损失算术平
声边界改变了原有的刚性边界条件，使陷波模态发 均值最大，达到了6.6 dB，因为吸声结构有效地抑制
生了变化，从而提高了插入损失。从图8 和图9 的结 了陷波模态。而扩散结构和楔形结构的插入损失算
果对比还可以发现，楔形结构和扩散结构可以显著 术平均值较小，分别为 1.6 dB 和 1.1 dB。原因在于