Page 110 - 《应用声学》2020年第6期

904 2020 年 11 月

系，此处选取了图 4 中 4 个插入损失曲线的波谷频 第 8 阶陷波模态共振频率。为了验证计算公式的准
率，即 180 Hz、350 Hz、520 Hz 和 690 Hz 频率处的 确性，表 1 列出了仿真模拟和公式计算的陷波模态
声场分布进行了分析，如图5所示。可以看到这4个 共振频率对比。结果表明，两组数据之间的偏差极
频率处的声场均出现了明显的简正模式，声波的传 小，意味着在确定了平行声屏障之间的几何条件之
播处于驻波状态，方向与平行声屏障垂直。绝大多 后，可以快速准确地通过公式对声屏障陷波模态的
数的声能被限制在顶端开口的结构内，极小部分的 共振频率进行计算，并提前采取控制措施。
声能扩散到外部空间。这大部分的声能垂直地入射
到声屏障顶端。根据几何衍射理论可知，对本文的 表 1 陷波模态的共振频率对比
研究对象而言，垂直入射声波的衍射系数最大 [15] 。 Table 1 Comparison of the resonance fre-
quencies of wave-trapping modes
因此平行声屏障的陷波模态处于共振频率时，接收
点的衍射声能达到极大值，插入损失取得极小值。
阶数 2 4 6 8
dB
2.5 140 仿真模拟/Hz 180 350 520 690
2.0 120
m 1.5 100
1.0 80 公式计算/Hz 172 344 516 688
0.5 60
0
0 1 2 3 4 5 6 7 8 9 3 插入损失优化
m
(a) 180 Hz
本节对3 种可能改善平行声屏障插入损失的优
dB
2.5 140
2.0 120 化方法进行了仿真分析。声屏障的构造如图6 所示，
m 1.5 100
1.0 80 包括内表面带楔形结构的声屏障、内表面带扩散型
0.5 60
0 声屏障和吸声型声屏障。其中，单个楔形结构的高
0 1 2 3 4 5 6 7 8 9
m
度为0.25 m，向下倾角为60 。扩散型结构按照二次
◦
(b) 350 Hz
余数扩散体 [16] 进行设计，所选为 7 阶扩散体，深度
dB
2.5 140
2.0 120 比值为 0 : 1 : 4 : 2 : 2 : 4 : 1，最大深度为 0.019 m，
m 1.5 100
1.0 80
0.5 60 60°
0
0 1 2 3 4 5 6 7 8 9 ഀॎፇ౞
m
(c) 520 Hz
dB
2.5 140 S
2.0 120
m 1.5 100 (a) ഀॎፇ౞
1.0 80
0.5 60
0
ੱஙፇ౞
0 1 2 3 4 5 6 7 8 9
m
(d) 690 Hz
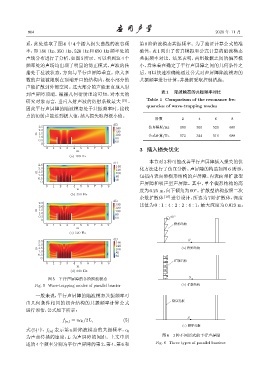
图 5 平行声屏障的各阶陷波模态 S
Fig. 5 Wave-trapping modes of parallel barrier (b) ੱஙፇ౞
一般来说，平行声屏障的陷波模态共振频率可
由几何条件相同的闭合结构的共振频率计算公式 ॲቈߘ౜
进行预估，公式如下所示：

S
f (n) = nc 0 /2L, (5)
(c) ॲቈߘ౜
式 (5) 中，f (n) 表示第 n 阶陷波模态的共振频率，c 0
为声音传播的速度，L 为声屏障的间距。上文中所 图 6 3 种不同形式的平行声屏障
述的4 个频率分别为平行声屏障的第2、第4、第6和 Fig. 6 Three types of parallel barriers