Page 31 - 《应用声学》2020年第6期

第 39 卷 第 6 期 张青青等： 南中国海海域存在孤立子内波条件下的声场统计特性 825

同时刻声速场的空间分布。作为例子，图6给出了根 声强，在 1/3 倍频程带宽内对多个频点的声强进行
据 S17 点上的温度链数据得到的 9 月 13 日 15:24:29 窄带平均，得到多个频点的平均声强：
时刻的声速场空间分布。 1 ∑
M
I(r, z) = I(f m ; r, z), (4)
M
ܦᤴ/(mSs -1 ) m=1
0 1545
其中，M 为频点个数。本文以窄带平均的传播损失
20 1540 (dB re 1 m)表示声场计算的数值结果：
ງए/m 40 1535 TL(r, z) = −10 lg I(r, z) . (5)
60
1530 I(r = 1)
80
1525 最后采用蒙特卡洛方法对模型计算的 TL 进行统计
100
0 2 4 6 8 10 12 14 分析，可获得概率统计结果。将接收点的TL数据每
ᡰሏ/km
隔1 dB分为一组，计算出每组的概率。假设TL 0 表
图 6 根 据 S17 点 温 度 链 数 据 得 到 的 9 月 13 日
示某个样本区间的中点，例如，当样本组区间范围为
15:24:29 时刻的声速场空间分布
[70 71]时，TL 0 = 70.5 dB。
Fig. 6 Spatial distribution of the sound speed field
based on the S17 site at 15:24:29 on September 13
ܦᤴ/(mSs -1 )
0
3 孤立子内波存在条件下的声场统计特性

利用温度链数据结合二维平流模型重构出随 ๒ ඵ
110
时空变化的海水中声速场分布后，可代入二维抛物 c  =1595.5 m/s
方程声场模型 [20] (RAM-PE) 计算内波存在条件下 ๒ງ/m ρ 2 =1.7 g/cm 3 1.07 dB/λ ොሥࡏ
α 2=0.517(f/1000)
不同时刻的声场。由于声波速度远远大于孤立子内 118
c  =1704 m/s
波的传播速度，声信号传播至接收潜标的时间内，内 ρ 3 =1.9 g/cm 3
α 3=0.517(f/1000) 1.07 dB/λ ۳अ
波的传播距离极为有限，所以可将内波场视为准静
态，使用RAM-PE模型结合海底参数模型计算声传
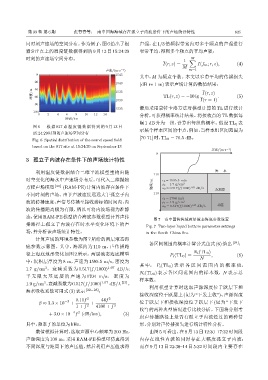
图 7 南中国海海域两层液态海底参数设置
播路径上孤立子内波存在时水平变化环境下的声
Fig. 7 Two-layer liquid bottom parameter settings
场，并分析该声场统计特性。 in the South China Sea
计算声场的环境参数为图 7 所给的两层液态海
各区间范围内概率计算公式由式(6)给出 [24] ：
底参数示意图。其中，海深约为 110 m，声传播路
径上海底地形变化如图 2 所示。两层液态海底模型 P i (TL 0 ) = N i (TL 0 ) , (6)
N
中：沉积层厚度为 8 m，声速为 1595.5 m/s，密度为
其 中， P i (TL 0 ) 表 示 各 区 间 范 围 内 的 概 率 值，
3
1.7 g/cm ，衰减系数为 0.517(f/1000) 1.07 dB/λ；
N i (TL 0 ) 表示各区间范围内的样本数，N 表示总
半 无 限 大 基 底 层 的 声 速 为 1704 m/s， 密 度 为
样本数。
3
1.9 g/cm ，衰减系数为0.517(f/1000) 1.07 dB/λ [21] 。
利用模型计算时选取声源深度位于跃层下和
海水吸收系数可用式(3)表示 [22−23] ：
接收深度位于跃层上 (记为 “下发上收”)、声源深度
0.11f 2 44f 2
−3
β ≈ 3.3 × 10 + + 位于跃层下和接收深度位于跃层下 (记为 “下发下
1 + f 2 4100 + f 2
收”)的两种典型情况进行比较分析。下面将分别考
+ 3.0 × 10 −4 2 (3)
f (dB/km),
虑声传播路径上是否有孤立子内波经过的两种情
其中，频率f 的单位为kHz。 形，分别对声传播损失进行统计特性分析。
数值模拟计算时，选取声源中心频率为200 Hz， 由图 5 可看出，在 9 月13 日12:30–17:32 时间段
声源深度为108 m。采用RAM-PE模型可仿真得到 内存在线性内波的同时存在大幅度孤立子内波；
不同深度与距离下的声压值，然后利用声压值求得 而在 9 月 13 日 23:30–14 日 5:32 时间段内主要存在