Page 34 - 《应用声学》2020年第6期

828 2020 年 11 月

为76 m。从图中可以看出，接收点声传播损失随时 场统计特性分析时，TL 概率分布在一定的区间范
间无规则起伏振荡。在图 14(a) 中声传播损失起伏 围内，且最大概率对应的 TL在区间中间，所以可用
最大约为 3 dB，图 14(b) 中声传播损失起伏最大约 概率分布的区间宽度衡量 TL 的分散程度。从图 15
为4 dB。 中可以看出，在有无孤立子内波经过时，图 15(a) 为
64 接收器位于跃层之上时(下发上收)，TL概率分布区
66
间宽度分别为 9 dB 和7 dB；图15(b) 为接收器位于
68
TL/dB 70 跃层之下时 (下发下收)，TL 概率分布区间宽度分
72
别为 12 dB 和7 dB，说明孤立子内波经过声传播路
74
76 径比不经过声传播路径条件下的 TL 概率分布更加
0 1.0 2.0 3.0 4.0 5.0
௑ᫎ/h 分散。
(a) ʾԧʽஆᄊৱц ଌஆງए˞22 m
64 0.6
66 0.5 ௄ߤቡߕЯฉፃ᣿ܦ͜୧᡹य़
దߤቡߕЯฉፃ᣿ܦ͜୧᡹य़
TL/dB 68 0.4
70
72
74
76 ഐဋ 0.3
0 1.0 2.0 3.0 4.0 5.0
௑ᫎ/h 0.2
(b) ʾԧʾஆᄊৱц ଌஆງए˞76 m
0.1
图 14 声传播路径上无孤立子内波经过时不同接收
0
点处声传播损失随时间变化的曲线 60 65 70 75 80
TL/dB
Fig. 14 Curve of the TLs when no soliton inter-
(a)ʾԧʽஆᄊৱц὘ଌஆງए˞22 m
nal waves entering the sound propagation path at
each receiving point 0.6
௄ߤቡߕЯฉፃ᣿ܦ͜୧᡹य़
比较图 11 和图 14 可知，当孤立子内波在声传 0.5 దߤቡߕЯฉፃ᣿ܦ͜୧᡹य़
播路径上移动时，接收点在短时间内声传播损失起 0.4
伏剧烈，声传播损失起伏最大相差可达 7∼8 dB；而 ഐဋ 0.3
无孤立子内波经过声传播路径时，接收点声场能量 0.2
起伏相对较小，最大相差为 3∼4 dB。文献 [18] 和文
0.1
献[25]指出，当孤立子内波经过声传播路径时，引起
0
声能量起伏与内波波阵面和声传播路径所成角度 60 65 70 75 80
TL/dB
有关，当角度较大时不同号简正波耦合是引起声能 (b)ʾԧʾஆᄊৱц὘ଌஆງए˞76 m
量起伏的主要因素。
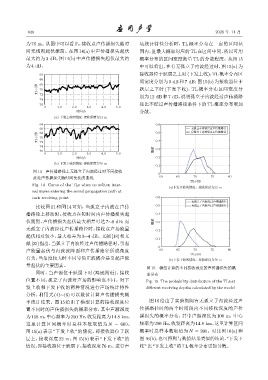
图 15 模型计算的不同接收深度的声传播损失的概
同时，当声源位于跃层下时 (海底附近)，接收 率分布
位置不同，孤立子内波对声场的影响也不同。对下 Fig. 15 The probability distribution of the TLs at
发上收和下发下收的两种情况进行声场统计特性 different receiving depths calculated by the model
分析，利用式 (4)∼(6) 可以数值计算声传播损失概
率统计结果。图 15 给出了模型计算的接收深度位 图 16 给出了实验期间有无孤立子内波经过声
置不同时的声传播损失的概率分布，其中声源深度 传播路径时的两个时间段内不同接收深度的声传
为108 m，中心频率为 200 Hz，收发距离为14.8 km， 播损失的概率分布，其中声源深度为 108 m，中心
这里计算区间概率时总样本数取值为 N = 600。 频率为 200 Hz，收发距离为 14.8 km，这里计算区间
图 15(a) 表示 “下发上收” 的情况，即接收器位于跃 概率时总样本数取值为 N = 200。对比图 16(a) 和
层上，接收深度 22 m；图 15(b) 表示 “下发下收” 的 图16(b)，也可得到与数值结果类似的结论，“下发下
情况，即接收器位于跃层下，接收深度76 m。进行声 收”比“下发上收”的TL概率分布更加分散。