Page 30 - 《应用声学》2020年第6期

824 2020 年 11 月

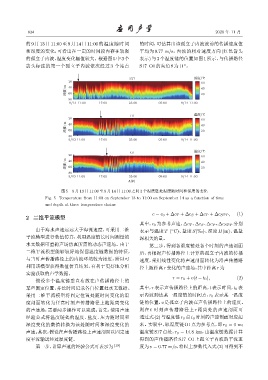
的 9 月 13 日 11:00 至 9 月 14 日 11:00 的温度随时间 的时间，可估算出该孤立子内波波前的传播速度值
和深度的变化，可看出在一定的时间段内存在较强 平均为 0.77 m/s，内波的相对速度方向 (红色箭头
的孤立子内波，温度变化幅值较大。根据图 5中3个 表示) 与 3 个温度链的位置如图 1 所示，与传播路径
箭头标注的第一个孤立子内波依次经过 3 个站点 S17–O1的夹角θ 为11 。
◦
S17 ພए/Ć
20 60
ງए/m 40 40
60
20
80
9/13 11:00 17:00 23:00 05:00 9/14 11:00
ພए/Ć
H1
20
60
ງए/m 40 40
60
20
80
9/13 11:00 17:00 23:00 05:00 9/14 11:00
ພए/Ć
O1
20 60
ງए/m 40 40
60
20
80
9/13 11:00 17:00 23:00 05:00 9/14 11:00
௑ᫎ
图 5 9 月 13 日 11:00 至 9 月 14 日 11:00 之间 3 个温度链处温度随时间和深度的变化
Fig. 5 Temperature from 11:00 on September 13 to 11:00 on September 14 as a function of time
and depth at three temperature chains

c = c 0 + ∆c T + ∆c S + ∆c P + ∆c ST P , (1)
2 二维平流模型
其中，c 0 为参考声速，∆c T 、∆c S 、∆c P 、∆c ST P 分别
由于海水声速远远大于海流速度，可采用二维 表示与温度 T ( C)、盐度 S(‰)、深度 H(m)、温盐
◦
平流模型进行数值仿真，利用温度链长时间测量的 深相关的量。
水文数据可重构声场仿真所需的动态声速场。由于 第二步，得到各温度链处各个时刻的声速剖面
二维平流模型能够较好地保留温度链数据的特征， 后，再根据声传播路径上计算的孤立子内波的传播
与当时声传播路径上的内波环境较为接近，所以可 速度，采用线性变化将声速剖面转化为沿声传播路
利用该模型获得数值仿真结果，有利于更好地分析 径上随距离r 变化的声速场，其中距离r 为
实验获取的声学数据。
r = r 0 + v(t − t 0 ), (2)
假设多个温度链垂直布放在声传播路径上的
某些固定位置，并长时间记录各自位置处水文数据。 其中，r 表示声传播路径上的距离，t 表示时间，t 0 表
采用二维平流模型将固定位置处随时间变化的温 示内波到达某一温度链的时间点，r 0 表示某一温度
度剖面转化为任意时刻声传播路径上随距离变化 链的位置，v 是孤立子内波在声传播路径上的速度。
的声速场，需要两步操作可以完成：首先，使用声速 则在 t 时刻声传播路径上 r 距离处的声速剖面可
经验公式将温度链处的温度、盐度、压力随时间和 通过式 (2)与温度链r 0 点t 0 时刻的声速剖面对应起
深度变化的数值转换为该处随时间和深度变化的 来。实验中，取温度链O1 点为参考点，即r 0 = 0 m；
声速；其次，假设在声传播路径上声速剖面以固定速 温度链 S17 点处，r 0 = 14.8 km，由温度链数据计算
度平流输送经过温度链。 得到的声传播路径 S17–O1 上孤立子内波的平流速
第一步，计算声速的经验公式可表示为 [19] 度为v = 0.77 m/s，将以上参数代入式(2)可得到不