Page 25 - 《应用声学》2020年第6期

第 39 卷 第 6 期 李天宇等： 拖曳阵被动合成孔径目标深度稳健估计 819

做到精确测量环境信息，因此仿真的波数位置与实 了估计结果的稳健性，当测量的环境信息与真实环
际波数位置存在偏差。在实际应用中，需要在仿真 境偏差大时，这种稳健性的下降会带来严重的误差
得到的波数位置附近选取距离仿真波数距离较近 问题。从另一个角度来看，实际上通常对水下目标
的峰值进行匹配。另外，模态匹配时阶数选择是一 进行深度估计时，分辨率并不是最主要考虑的性能，
个需要考虑的问题，增加模态匹配的阶数，可以在一 因此实际应用中倾向于选择较少阶数的模态进行
定程度上提高目标深度估计分辨率，但同时也降低 匹配。

5 5
വগͥᝠፇ౧ വগͥᝠፇ౧
͌ᄾവগฉ஝ ኄ3᫽ ͌ᄾവগฉ஝
0 0 ኄ3᫽
ኄ2᫽ ኄ2᫽
-5 -5
ࣨϙ/dB -10 ࣨϙ/dB -10

-15 -15
-20 -20

-25 -25
0.70 0.75 0.80 0.85 0.70 0.75 0.80 0.85
ฉ஝/m -1 ฉ஝/m -1
(a) ፃ᣿ઈࣰ੸ᮕܫေ (b) ళፃઈࣰ੸ᮕܫေ
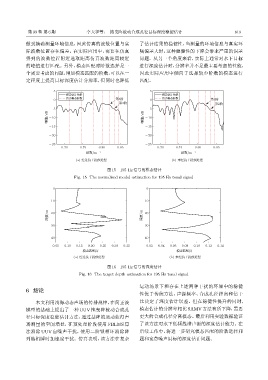
图 15 195 Hz 信号的模态估计
Fig. 15 The normalized modal estimation for 195 Hz tonal signal

0 0

10 10

ງए/m 20 ງए/m 20

30 30

40 40

0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.02 0.04 0.06 0.08 0.10 0.12 0.14
വগӜᦡए വগӜᦡए
(a) ፃ᣿ઈࣰ੸ᮕܫေ (b) ళፃઈࣰ੸ᮕܫေ
图 16 195 Hz 信号的深度估计
Fig. 16 The target depth estimation for 195 Hz tonal signal

运动场景下和存在上述两种干扰的环境中的稳健
6 结论
性优于传统方法，声源频率、合成孔径距离和信干
本文利用浅海动态声场的传播规律，在简正波 比决定了深度估计误差。但在稳健性提升的同时，
模型的基础上提出了一种 UUV 拖曳阵被动合成孔 模态估计的分辨率相比 SAMV方法有所下降，需要
径目标深度稳健估计方法，通过基阵的运动获得声 更大的合成孔径分离模态。最后利用实验数据验证
场测量的空间增益，在预处理阶段使用 FBLMS 算 了该方法对水下低频线谱声源的深度估计能力。在
法消除 UUV 自噪声干扰，使用二阶锁相环消除阵 后续工作中，将进一步研究模态匹配的阶数选择问
列随机瞬时加速度干扰。仿真表明，该方法在复杂 题和宽带噪声目标的深度估计问题。