Page 21 - 《应用声学》2020年第6期

第 39 卷 第 6 期 李天宇等： 拖曳阵被动合成孔径目标深度稳健估计 815

速度匀速运动。拖曳阵先做匀加速运动再做匀减
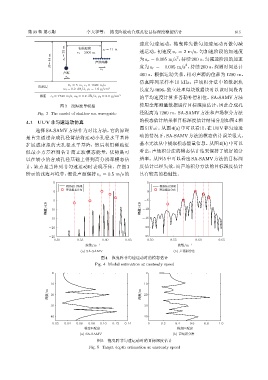
z s=23 m r  =2000 m z r =11 m 速运动，初速度 v r = 2 m/s，匀加速阶段的加速度
Ѻݽᡰሏ
H =44 m ܦጪ۳᫼ 为 a r = 0.005 m/s ，持续 200 s，匀减速阶段的加速
2
2
v r 度为 a r = −0.005 m/s ，持续 200 s，探测时间总计
ܦູ 400 s。根据运动关系，相对声源的位移为 1200 m。
v s
仿真阵列采样率 10 kHz。声场积分法中的数据块
ොሥࡏ H =5 m, c =1620 m/s
α  =0.2 dB/λ, ρ  =1.6 g/cm 3 长度为 4096，独立处理每块数据块时以该时间段内
๒अ c b =1740 m/s, α b =0.2 dB/λ, ρ b =2.0 g/cm 3 的平均速度计算多普勒补偿相位。SA-SAMV 方法

图 3 浅海波导模型 使用全部测量数据进行目标深度估计，因此合成孔
Fig. 3 The model of shallow sea waveguide 径距离为1200 m。SA-SAMV方法和声场积分方法
4.1 UUV非匀速运动仿真 的模态估计结果和目标深度估计结果分别如图 4 和
图 5 所示。从图 4(a) 中可以看出，在UUV 非匀速运
选择 SA-SAMV 方法作为对比方法，它的原理
动的情况下，SA-SAMV 方法的模态估计误差很大，
是首先通过合成孔径算法将运动小孔径水平基阵
扩展成虚拟的大孔径水平基阵，然后利用稀疏近 基本无法从中提取模态能量信息。从图4(b)中可以
似最小方差准则估计简正波模态能量，优势是可 看出，声场积分法的模态估计结果保持了较好的分
以在较小的合成孔径基础上得到高分辨率模态估 辨率。从图 5 中可以看出 SA-SAMV 方法的目标深
计，缺点是当阵列非匀速运动时表现不佳。在图 3 度估计已经失效，而声场积分方法的目标深度估计
所示的浅海环境中，假设声源保持 v s = 0.5 m/s 的 具有较高的稳健性。
5 5
വগͥᝠፇ౧ വগͥᝠፇ౧
ေ᝷വগѬ࣋ ေ᝷വগѬ࣋
0 0
-5 -5
ࣨϙ/dB -10 ࣨϙ/dB -10

-15 -15

-20 -20
-25 -25
0.50 0.55 0.60 0.65 0.50 0.55 0.60 0.65
ฉ஝/m -1 ฉ஝/m -1
(a) SA¹SAMV (b) ܦڤሥѬข
图 4 拖曳阵非匀速运动时的模态估计
Fig. 4 Modal estimation at unsteady speed
0 0

10 10
ງए/m 20 ງए/m 20

30 30

40 40
0.02 0.04 0.06 0.08 0.10 0.12 0.14 0 0.2 0.4 0.6 0.8 1.0
വগӜᦡए വগӜᦡए
(a) SA¹SAMV (b) ܦڤሥѬข
图 5 拖曳阵非匀速运动时的目标深度估计
Fig. 5 Target depth estimation at unsteady speed