Page 24 - 《应用声学》2020年第6期

818 2020 年 11 月

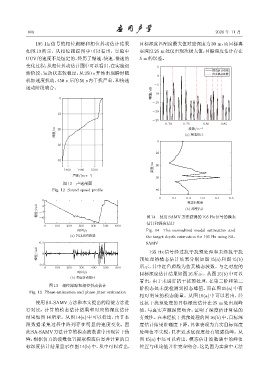
195 Hz 信号的相位跟踪和相位抖动估计结果 目标深度匹配度最大值对应深度为30 m，而目标真
如图 13 所示，从相位跟踪图中可以看出，实验中 实深度25 m处仅出现次极大值，目标深度估计存在
UUV的速度不是恒定的，经历了慢速-快速-慢速的 5 m的误差。
变化过程；从相位抖动估计图中可以看出，在实验初 5
വগͥᝠፇ౧
始阶段，运动状态较稳定，从 250 s 开始出现瞬时随 ͌ᄾവগฉ஝
0
机加速度扰动，450 s 后的 50 s 内干扰严重，和快速
-5
运动阶段吻合。
ࣨϙ/dB -10
0
-15
-20
10
-25
0.70 0.75 0.80 0.85
ງए/m 20 (a) വগͥᝠ
-1
ฉ஝/m
0
30
10
40
ງए/m 20
1460 1480 1500
ܦᤴ/(mSs -1 )
30
图 12 声速剖面
Fig. 12 Sound speed profile 40
0 0.1 0.2 0.3 0.4 0.5
0
വগӜᦡए
ᄱͯ/rad -4 图 14 使用 SAMV 方法获得的 195 Hz 信号的模态
-2
(b) ງएͥᝠ
-6
估计和深度估计
0 100 200 300 400 500 600
௑ᫎ/s Fig. 14 The normalized modal estimation and
(a) PLLᄱͯᡲᢎ the target depth estimation for 195 Hz using SA-
0.5 SAMV
ᄱͯ/rad 0 预处理的模态估计结果分别如图 15(a) 和图 15(b)
195 Hz 信号经过抗干扰预处理和未经抗干扰

-0.5 所示，其中红色虚线为仿真模态波数。与之对应的
0 100 200 300 400 500 600
௑ᫎ/s
目标深度估计结果如图 16所示。从图 15(b) 中可以
(b) ᄱͯઇүͥᝠ
看出，由于未进行抗干扰预处理，在第二阶和第三
图 13 相位跟踪和相位抖动估计
阶模态处未能检测到模态峰值，而在图 15(a) 中有
Fig. 13 Phase estimation and phase jitter estimation
相对明显的模态能量。从图 16(a) 中可以看出，经
使用SA-SAMV方法和本文提出的稳健方法进 过抗干扰预处理的目标深度估计在 25 m 处出现峰
行对比，计算的模态估计结果和对应的深度估计 值，与真实声源深度吻合，证明了深度估计算法的
结果如图 14 所示。从图 14(a) 中可以看出，由于本 有效性。在未经抗干扰预处理的图16(b)中，目标深
段数据采集过程中阵列存在明显的速度变化，因 度估计结果准确度下降，具体表现为真实目标深度
此SA-SAMV方法计算的模态波数谱中出现若干伪 处峰值不尖锐，且在近水底深度处有较强伪峰。从
峰，根据仿真的波数位置提取模态信息并计算的目 图 15(a) 中还可以看出，模态估计波数谱中的峰值
标深度估计结果显示在图 14(b) 中，从中可以看出， 位置与理论值并非完全吻合，这是因为实验中无法