Page 23 - 《应用声学》2020年第6期

第 39 卷 第 6 期 李天宇等： 拖曳阵被动合成孔径目标深度稳健估计 817

4.3 深度估计误差的影响因素 从图 10 中可以看出，声源频率一定时，目标深度估
为进一步研究目标深度估计误差的影响因素， 计误差随合成孔径的增加而减小，当合成孔径距离
假设准确测量了环境信息，在 4.2 节中的自噪声干 足够大时，目标深度估计误差不再进一步随合成孔
扰下使用声场积分方法进行目标深度估计。声源频 径的增加而减小；当合成孔径和信干比一定时，目标
率为 145 Hz 和 245 Hz，以自噪声作为干扰源定义 深度估计误差与声源频率有关，对低频声源的模态
的信干比变化范围为 −20 ∼ 20 dB，合成孔径距离 估计更准确，这是因为低频声源激发的简正波阶数
为 1000 m，通过 100 次 Monte Carlo 仿真得到经过 较少，波数间隔较大，易于分辨和估计。在实际应用
ANC和未经ANC的目标深度估计误差如图9所示， 中往往存在多目标，根据探测到的目标相对阵列的
从图9 中可以看出，ANC 预处理可以显著降低自噪 方向，可以对不同方向的目标并行地计算其声压的
声干扰导致的目标深度估计误差，如果不经过ANC 空间分布。由于式 (8) 利用波数域阵处理获得了阵
预处理，当信干比低于 0 dB时，误差明显增大，导致 增益，阵列的阵元数越多则阵增益越高，因此在计算
目标深度估计失效。经过 ANC 预处理可以在更低 某个方向的目标的模态估计波数谱时，来自非当前
信干比实现目标深度估计。在信干比固定为 10 dB 方向的其他目标的信号可以等效为波数域的噪声。
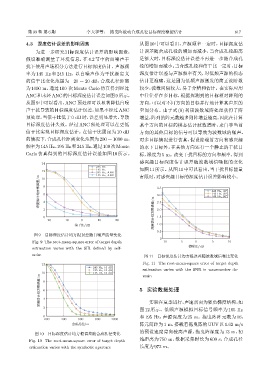
的情况下，合成孔径距离变化范围为200 ∼ 1000 m， 对多目标情况进行仿真，假设除端射方向有感兴趣
频率为145 Hz、195 Hz和245 Hz，通过100次Monte 的水下目标外，在其他方向还有一个静止的干扰目
Carlo 仿真得到的目标深度估计误差如图 10 所示。 标，深度为 5 m。改变干扰目标的方向和频率，得到
感兴趣目标深度估计误差随波数域信噪比的变化
14
245 Hz
145 Hz 如图11所示。从图 11中可以看出，当干扰目标能量
12
245 Hz, ANC
145 Hz, ANC 有限时，对感兴趣目标的深度估计误差影响较小。
ງएͥᝠکவಪឨࣀ/m 8 6 3.5 245 Hz, 30°
10
145 Hz, 30°
3.0
145 Hz, 60°

2 4 2.5
2.0
0 ງएͥᝠکவಪឨࣀ/m 1.5
-20 -10 0 10 20
ηࣰඋ/dB 1.0
0.5
图 9 目标深度估计均方根误差随自噪声能量变化
0
Fig. 9 The root-mean-square error of target depth -10 -5 0 5 10
η٪උ/dB
estimation varies with the SIR defined by self-
noise 图 11 目标深度估计均方根误差随波数域信噪比变化

12 Fig. 11 The root-mean-square error of target depth
245 Hz, 10 dB
195 Hz, 10 dB estimation varies with the SNR in wavenumber do-
10 145 Hz, 10 dB main
ງएͥᝠکவಪឨࣀ/m 8 6 4 5 实验数据处理

2 实验在夏季进行，声速剖面为强负梯度结构，如
图 12 所示。低频声源模拟目标信号频率为 165 Hz
0 和 195 Hz，声源深度为 25 m。拖曳阵阵元数为 16，
200 400 600 800 1000
Ռੇߘय़/m 阵元间距为 1 m，搭载着拖曳阵的UUV 以1.62 m/s
的预设速度背向驶离声源，拖曳阵深度为 13 m，初
图 10 目标深度估计均方根误差随合成孔径变化
Fig. 10 The root-mean-square error of target depth 始距离为 750 m，数据采集时长为 600 s，合成孔径
estimation varies with the synthetic aperture 长度为972 m。